题目内容
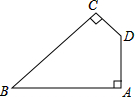 如图,四边形ABCD中,∠A=∠BCD=90°,∠ABC=45°,AD=1,AB=4,求四边形ABCD的面积.
如图,四边形ABCD中,∠A=∠BCD=90°,∠ABC=45°,AD=1,AB=4,求四边形ABCD的面积.考点:勾股定理
专题:
分析:延长AD、BC相交于点E,判断出△ABE是等腰直角三角形,再根据直角三角形两锐角互余求出∠E=45°,然后判断出△CDE是等腰直角三角形,然后求出DE再求出CE,最后根据S四边形ABCD=S△ABE-S△CDE列式计算即可得解.
解答: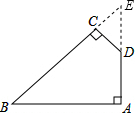 解:如图,延长AD、BC相交于点E,
解:如图,延长AD、BC相交于点E,
∵∠A=90°,∠ABC=45°,
∴△ABE是等腰直角三角形,
∴∠E=45°,AE=AB=4,
∵AD=1,
∴DE=AE-AD=4-1=3,
∵∠BCD=90°,
∴△CDE是等腰直角三角形,
∴CE=
DE=
×3=
,
∴S四边形ABCD=S△ABE-S△CDE
=
×4×4-
×
×
=8-
,
=
.
 解:如图,延长AD、BC相交于点E,
解:如图,延长AD、BC相交于点E,∵∠A=90°,∠ABC=45°,
∴△ABE是等腰直角三角形,
∴∠E=45°,AE=AB=4,
∵AD=1,
∴DE=AE-AD=4-1=3,
∵∠BCD=90°,
∴△CDE是等腰直角三角形,
∴CE=
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
∴S四边形ABCD=S△ABE-S△CDE
=
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
=8-
| 9 |
| 4 |
=
| 23 |
| 4 |
点评:本题考查了勾股定理,等腰直角三角形的判定与性质,三角形的面积,作辅助线构造出等腰直角三角形是解题的关键.

练习册系列答案
相关题目
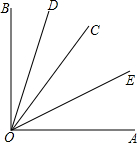 如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数.
如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数. 如图,∠AOD=120°,∠DOC=∠COB,∠AOC=75°.
如图,∠AOD=120°,∠DOC=∠COB,∠AOC=75°. C为线段AB上的点,DA、EB、CF均垂直于AB,且DA=CB,EB=AC,CF=AB.求证:∠AFD=∠BFE.
C为线段AB上的点,DA、EB、CF均垂直于AB,且DA=CB,EB=AC,CF=AB.求证:∠AFD=∠BFE. 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,AD平分∠BAC交BC于D,则BD的长为
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,AD平分∠BAC交BC于D,则BD的长为