题目内容
 如图是我省某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9m,AB=36m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为5m,则DE的长为
如图是我省某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9m,AB=36m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为5m,则DE的长为考点:二次函数的应用
专题:
分析:首先建立平面直角坐标系,设AB与y轴交于H,求出OC的长,然后设设该抛物线的解析式为:y=ax2+k,根据题干条件求出a和k的值,再令y=0,求出x的值,即可求出D和E点的坐标,DE的长度即可求出.
解答:解:如图所示,建立平面直角坐标系.
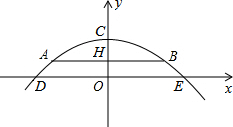
设AB与y轴交于点H,
∵AB=36,
∴AH=BH=18,
由题可知:
OH=5,CH=9,
∴OC=9+5=14,
设该抛物线的解析式为:y=ax2+k,
∵顶点C(0,14),
∴抛物线y=ax2+14,
代入点(18,5)
∴5=18×18a+14,
∴5=324a+14,
∴324a=-9,
∴a=-
,
∴抛物线:y=-
x2+14,
当y=0时,0=-
x2+14,
∴-
x2=-14,
∴x2=14×36=504,
∴x=±6
,
∴E(6
,0),D(-6
,0),
∴OE=OD=6
,
∴DE=OD+OE=6
+6
=12
,
故答案为:12
.

设AB与y轴交于点H,
∵AB=36,
∴AH=BH=18,
由题可知:
OH=5,CH=9,
∴OC=9+5=14,
设该抛物线的解析式为:y=ax2+k,
∵顶点C(0,14),
∴抛物线y=ax2+14,
代入点(18,5)
∴5=18×18a+14,
∴5=324a+14,
∴324a=-9,
∴a=-
| 1 |
| 36 |
∴抛物线:y=-
| 1 |
| 36 |
当y=0时,0=-
| 1 |
| 36 |
∴-
| 1 |
| 36 |
∴x2=14×36=504,
∴x=±6
| 14 |
∴E(6
| 14 |
| 14 |
∴OE=OD=6
| 14 |
∴DE=OD+OE=6
| 14 |
| 14 |
| 14 |
故答案为:12
| 14 |
点评:本题主要考查二次函数综合应用的知识点,解答本题的关键是正确地建立平面直角坐标系,此题难度一般,是一道非常好的试题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 二次函数y=ax2+bx+c的图象如图,点(-
二次函数y=ax2+bx+c的图象如图,点(-| b |
| a |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,以AB为直径的⊙O经过点C,点D为CO延长线上一点,且BC=BD,AB=4.
如图,以AB为直径的⊙O经过点C,点D为CO延长线上一点,且BC=BD,AB=4. 如图是一块直角三角形板材,其中,∠C=90°,AC=8cm,BC=6cm,请问:如何从这块板材上裁剪下一块面积最大的正方形?请画出你的设计图,并求出这块正方形的边长.
如图是一块直角三角形板材,其中,∠C=90°,AC=8cm,BC=6cm,请问:如何从这块板材上裁剪下一块面积最大的正方形?请画出你的设计图,并求出这块正方形的边长.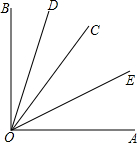 如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数.
如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数. 如图,∠AOD=120°,∠DOC=∠COB,∠AOC=75°.
如图,∠AOD=120°,∠DOC=∠COB,∠AOC=75°.