题目内容
5.下列命题中正确的是( )| A. | 正五边形是中心对称图形 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 化简-a$\sqrt{-\frac{1}{a}}$的结果是$\sqrt{-a}$ | |
| D. | 顺次连接对角线互相垂直的四边形各边中点所得的四边形是菱形 |
分析 A、根据中心对称图形的概念进行判断;B、根据垂径定理进行判断;C、判断a的正负,再化简即可判断;D、根据菱形和矩形的性质即可判断.
解答 解:A、正五边形不是中心对称图形,此选项错误;
B、当被平分的弦为直径时,两直径不一定垂直,此选项错误;
C、化简-a$\sqrt{-\frac{1}{a}}$的结果是$\sqrt{-a}$,此选项正确;
D、顺次连接对角线互相垂直的四边形各边中点所得的四边形是矩形,此选项错误;
故选C.
点评 本题主要考查了命题与定理的知识,解题的关键是掌握中心对称图形的概念以及四边形的相关知识,此题难度不大.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
13. 如图,a∥b,等边△ABC的顶点B在直线b上,∠1=20°,则∠2的度数为( )
如图,a∥b,等边△ABC的顶点B在直线b上,∠1=20°,则∠2的度数为( )
 如图,a∥b,等边△ABC的顶点B在直线b上,∠1=20°,则∠2的度数为( )
如图,a∥b,等边△ABC的顶点B在直线b上,∠1=20°,则∠2的度数为( )| A. | 60° | B. | 45° | C. | 40° | D. | 30° |
20.下列各式计算正确的是( )
| A. | a2+2a3=3a5 | B. | a•a2=a3 | C. | a6÷a2=a3 | D. | (a2)3=a5 |
15.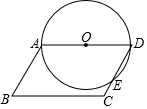 如图,?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则$\widehat{DE}$的长为( )
如图,?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则$\widehat{DE}$的长为( )
 如图,?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则$\widehat{DE}$的长为( )
如图,?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则$\widehat{DE}$的长为( )| A. | $\frac{1}{3}$π | B. | $\frac{2}{3}$π | C. | $\frac{7}{6}$π | D. | $\frac{4}{3}$π |
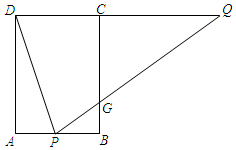 如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.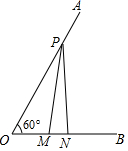 如图,已知∠AOB=60°,点P在边OA上,OP=10,点M、N在边OB上,PM=PN,若MN=2,则OM=( )
如图,已知∠AOB=60°,点P在边OA上,OP=10,点M、N在边OB上,PM=PN,若MN=2,则OM=( )