题目内容
15.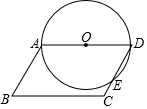 如图,?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则$\widehat{DE}$的长为( )
如图,?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则$\widehat{DE}$的长为( )| A. | $\frac{1}{3}$π | B. | $\frac{2}{3}$π | C. | $\frac{7}{6}$π | D. | $\frac{4}{3}$π |
分析 连接OE,由平行四边形的性质得出∠D=∠B=70°,AD=BC=6,得出OA=OD=3,由等腰三角形的性质和三角形内角和定理求出∠DOE=40°,再由弧长公式即可得出答案.
解答 解: 连接OE,如图所示:
连接OE,如图所示:
∵四边形ABCD是平行四边形,
∴∠D=∠B=70°,AD=BC=6,
∴OA=OD=3,
∵OD=OE,
∴∠OED=∠D=70°,
∴∠DOE=180°-2×70°=40°,
∴$\widehat{DE}$的长=$\frac{40π×3}{180}$=$\frac{2}{3}π$;
故选:B.
点评 本题考查了弧长公式、平行四边形的性质、等腰三角形的性质等知识;熟练掌握平行四边形的性质,求出∠DOE的度数是解决问题的关键.

练习册系列答案
相关题目
5.下列命题中正确的是( )
| A. | 正五边形是中心对称图形 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 化简-a$\sqrt{-\frac{1}{a}}$的结果是$\sqrt{-a}$ | |
| D. | 顺次连接对角线互相垂直的四边形各边中点所得的四边形是菱形 |
6.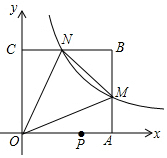 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )| A. | 6$\sqrt{2}$ | B. | 10 | C. | 2$\sqrt{26}$ | D. | 2$\sqrt{29}$ |
10.下列国旗图案是轴对称图形但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7. 如图的几何体由五个相同的小正方体搭成,它的主视图是( )
如图的几何体由五个相同的小正方体搭成,它的主视图是( )
 如图的几何体由五个相同的小正方体搭成,它的主视图是( )
如图的几何体由五个相同的小正方体搭成,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
 七(1)班举行投篮比赛,每人投5球.如图是全班学生投进球数的扇形统计图,则投进球数的众数是3球.
七(1)班举行投篮比赛,每人投5球.如图是全班学生投进球数的扇形统计图,则投进球数的众数是3球.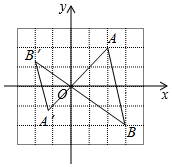 如图,在直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是(-2,$\frac{4}{3}$).
如图,在直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是(-2,$\frac{4}{3}$).