题目内容
9.无锡某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
分析 (1)根据:月销售量=原销售量+50×$\frac{原售价-实际售价}{10}$,即可列出函数关系式;根据供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售,列一元一次不等式组求解即可得x的取值.
(3)根据:总利润=每台利润×销售量,列出函数关系式,将函数关系式配方,即可求出最大w.
解答 解:(1)根据题中条件销售价每降低10元,月销售量就可多售出50台,
则月销售量y(台)与售价x(元/台)之间的函数关系式:y=200+50×$\frac{400-x}{10}$,
化简得:y=-5x+2200;
供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台,
则$\left\{\begin{array}{l}x≥300\\-5x+2200≥450\end{array}$,
解得:300≤x≤350.
∴y与x之间的函数关系式为:y=-5x+2200(300≤x≤350);
(2)W=(x-200)(-5x+2200),
整理得:W=-5(x-320)2+72000.
∵x=320在300≤x≤350内,
∴当x=320时,最大值为72000,
答:售价定为320元/台时,商场每月销售这种空气净化器所获得的利润w最大,最大利润是72000元.
点评 本题主要考查对于二次函数的应用和掌握,而且还应用到将函数变形求函数极值的知识,解题的关键是能够从实际问题中整理出二次函数模型.

练习册系列答案
相关题目
7.下列运算正确的是( )
| A. | a•a2=a3 | B. | 3a+2a2=5a2 | C. | 2-3=-8 | D. | $\sqrt{9}$=±3 |
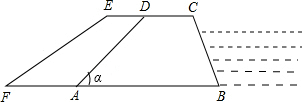 如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度(即tanα)为1:1.2,坝高10米,为了提高坝的防洪能力,由相关部门决定加固堤坝,要求将坝顶CD加宽2米,形成新的背水坡EF,其坡度为1:1.4,已知堤坝总长度为1000米.
如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度(即tanα)为1:1.2,坝高10米,为了提高坝的防洪能力,由相关部门决定加固堤坝,要求将坝顶CD加宽2米,形成新的背水坡EF,其坡度为1:1.4,已知堤坝总长度为1000米.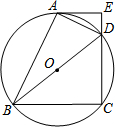 如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.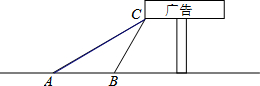 如图,某学校数学兴趣小组想了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到达点B处,又测得C点的仰角为60°.请你根据以上数据求广告牌底端C点离地面的高度.(结果保留根号)
如图,某学校数学兴趣小组想了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到达点B处,又测得C点的仰角为60°.请你根据以上数据求广告牌底端C点离地面的高度.(结果保留根号) 现要建造一段铁路,其路基的横断面ABCD是等腰梯形,上底CD=8米,高DH为2.5米,坡度i=1:1.2.
现要建造一段铁路,其路基的横断面ABCD是等腰梯形,上底CD=8米,高DH为2.5米,坡度i=1:1.2.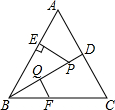 如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.如果BF=a,那么PE=$\frac{\sqrt{3}}{2}$a(用含a的代数式表示).
如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.如果BF=a,那么PE=$\frac{\sqrt{3}}{2}$a(用含a的代数式表示).