题目内容
17.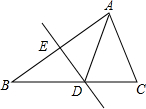 如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=15cm,△ADC的周长为40cm,求BC的长.
如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=15cm,△ADC的周长为40cm,求BC的长.
分析 首先根据折叠的性质,可得AD=BD;然后在△ADC中,用△ADC的周长减去AC的长度,求出AD和DC的长度和;最后根据AD=BD,求出BD和DC的长度和,即可求出BC的长是多少.
解答 解:根据折叠的性质,可得AD=BD;
∵△ADC的周长为40cm,AC=15cm,
∴AD+DC=40-15=25(cm),
∵AD=BD,
∴BD+DC=AD+DC=25(cm),
即BC的长为25cm.
点评 此题主要考查了翻转变换(折叠问题),解答此题的关键是要明确折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,并能判断出AD=BD.

练习册系列答案
相关题目
5. 如图图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又散步走回家,图中x表示时间,y表示张强离家的距离.则下列说法错误的是( )
如图图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又散步走回家,图中x表示时间,y表示张强离家的距离.则下列说法错误的是( )
 如图图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又散步走回家,图中x表示时间,y表示张强离家的距离.则下列说法错误的是( )
如图图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又散步走回家,图中x表示时间,y表示张强离家的距离.则下列说法错误的是( )| A. | 体育场离张强家2.5km | |
| B. | 张强从家到体育场用了15min | |
| C. | 张强在体育场锻炼了15min | |
| D. | 张强散步回家的平均速度是2.5km/h |
12. 如图,Rt△ABC中,∠C=90°,AC=8,BC=6,点是AB上的一个动点(不与A,B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况( )
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,点是AB上的一个动点(不与A,B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况( )
 如图,Rt△ABC中,∠C=90°,AC=8,BC=6,点是AB上的一个动点(不与A,B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况( )
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,点是AB上的一个动点(不与A,B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况( )| A. | 先增大后减少 | B. | 先减少后增大 | C. | 逐渐增大 | D. | 逐渐减少 |
9.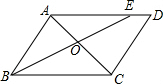 如图,在平行四边形ABCD中,点E在AD上,已知AE=3ED=6cm,OC=4cm,则AC的长为( )
如图,在平行四边形ABCD中,点E在AD上,已知AE=3ED=6cm,OC=4cm,则AC的长为( )
 如图,在平行四边形ABCD中,点E在AD上,已知AE=3ED=6cm,OC=4cm,则AC的长为( )
如图,在平行四边形ABCD中,点E在AD上,已知AE=3ED=6cm,OC=4cm,则AC的长为( )| A. | 9cm | B. | 7cm | C. | 6cm | D. | 8cm |
7. 如图,已知阴影部分是一个正方形,AB=4,∠B=45°,此正方形的面积( )
如图,已知阴影部分是一个正方形,AB=4,∠B=45°,此正方形的面积( )
 如图,已知阴影部分是一个正方形,AB=4,∠B=45°,此正方形的面积( )
如图,已知阴影部分是一个正方形,AB=4,∠B=45°,此正方形的面积( )| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
 如图,阴影部分(正方形)的四个顶点在5×5的网格格点上.
如图,阴影部分(正方形)的四个顶点在5×5的网格格点上.