题目内容
12. 如图,Rt△ABC中,∠C=90°,AC=8,BC=6,点是AB上的一个动点(不与A,B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况( )
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,点是AB上的一个动点(不与A,B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况( )| A. | 先增大后减少 | B. | 先减少后增大 | C. | 逐渐增大 | D. | 逐渐减少 |
分析 设DE=λ,运用相似三角形的性质,将矩形DECF的周长表示为λ的一次函数的形式,运用函数的性质即可解决问题
解答 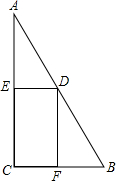 解:设DE=λ,DF=μ;
解:设DE=λ,DF=μ;
∵DE⊥AC于点E,DF⊥BC于点F,
∴四边形DECF为矩形,
∴CF=DE=λ,CE=DF=μ,
∴矩形DECF的周长η=2λ+2μ;
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{λ}{BC}$=$\frac{AD}{AB}$①;同理可证$\frac{μ}{AC}$=$\frac{BD}{AB}$②,
由①+②得:$\frac{λ}{6}$$+\frac{μ}{8}$=1,
∴μ=8-$\frac{4}{3}$λ
∴η=2λ+16-$\frac{8}{3}$λ,
=-$\frac{2}{3}$λ+16,
∵-$\frac{2}{3}$<0,
∴η随λ的增大而减小;
∵点D从靠近点A的某一点向点B移动时,λ逐渐变大,
∴矩形DECF的周长η逐渐减小.
故选D.
点评 该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
4.某校计划租用7辆客车,送八年级师生去南湖参观一大会址.现有甲、乙两种型号的客车可供选择,它们的载客量和租金如下表所示.设租用甲种客车x辆,租用总费用为y元.
(1)求出y(元)与x(辆)之间的函数表达式;
(2)若要求租车总费用不超过6500元,问有几种租车方案?哪种方案能使总载客量最大?
| 类别 | 甲种客车 | 乙种客车 |
| 载客量(人/辆) | 45 | 30 |
| 租金(元/辆) | 1000 | 800 |
(2)若要求租车总费用不超过6500元,问有几种租车方案?哪种方案能使总载客量最大?
1.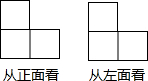 如图,是由若干个完全相同的小正方体组成的一个几何体的从正面看和从左面看的图形,则组成这个几何体的小正方体的个数是( )
如图,是由若干个完全相同的小正方体组成的一个几何体的从正面看和从左面看的图形,则组成这个几何体的小正方体的个数是( )
 如图,是由若干个完全相同的小正方体组成的一个几何体的从正面看和从左面看的图形,则组成这个几何体的小正方体的个数是( )
如图,是由若干个完全相同的小正方体组成的一个几何体的从正面看和从左面看的图形,则组成这个几何体的小正方体的个数是( )| A. | 3个或4个或5个 | B. | 4个或5个 | C. | 5个或6个 | D. | 6个或7个 |
2.以下四组木棒中,哪一组的三条能够刚好做成直角三角形的木架( )
| A. | 7厘米,12厘米,15厘米 | B. | 7厘米,12厘米,13厘米 | ||
| C. | 8厘米,15厘米,16厘米 | D. | 3厘米,4厘米,5厘米 |
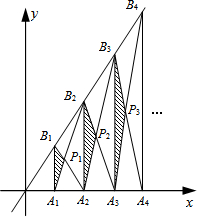 已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=2x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2 B3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn.若△A1B1P1,△A2B2P2,△A3B3P3,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn为$\frac{{n}^{2}}{2n+1}$.
已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=2x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2 B3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn.若△A1B1P1,△A2B2P2,△A3B3P3,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn为$\frac{{n}^{2}}{2n+1}$.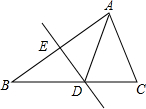 如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=15cm,△ADC的周长为40cm,求BC的长.
如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=15cm,△ADC的周长为40cm,求BC的长.