题目内容
9. 如图为y=ax2+bx+c的图象,则( )
如图为y=ax2+bx+c的图象,则( )| A. | a>0,b<0 | B. | a>0,b>0 | C. | b<0,c<0 | D. | a<0,c<0 |
分析 由抛物线的开口方向可确定a的符号,由抛物线的对称轴相对于y轴的位置可得a与b之间的符号关系,由抛物线与y轴的交点位置可确定c的符号.
解答 解:由抛物线的开口向上可得a>0;
由抛物线的对称轴在y轴的左边可得x=-$\frac{b}{2a}$<0,
则a与b同号,因而b>0;
由抛物线与y轴的交点在y轴的负半轴上可得c<0.
故选B.
点评 本题主要考查二次函数图象与系数的关系,其中a决定于抛物线的开口方向,b决定于抛物线的开口方向及抛物线的对称轴相对于y轴的位置,c决定于抛物线与y轴的交点位置.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知点M(3,2)与点N(a,b)在同一条平行于x轴的直线上,且点N到y轴的距离为4,那么点N的坐标是( )
| A. | (4,-2)或(-5,2) | B. | (4,-2)或(-4,-2) | C. | (4,2)或(-4,2) | D. | (4,2)或(-1,2) |
19.△ABC中,∠C=90°,∠A的平分线交BC于点D,如果AB=8,CD=3,则△ABD的面积为( )
| A. | 24 | B. | 12 | C. | 8 | D. | 6 |
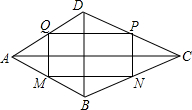 已知:如图,在四边形ABCD中,AB=AD,CB=CD,点M,N,N,P,Q分别是AB,BC,CD,DA的中点,求证:四边形MNPQ是矩形.
已知:如图,在四边形ABCD中,AB=AD,CB=CD,点M,N,N,P,Q分别是AB,BC,CD,DA的中点,求证:四边形MNPQ是矩形.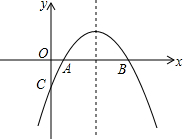 如图抛物线y=-x2+bx+c与x轴的两个交点别为A(1,0),B(3,0)
如图抛物线y=-x2+bx+c与x轴的两个交点别为A(1,0),B(3,0) 已知:AC平分∠DAB,∠DAB+∠DCB=180°,若CE:CB=5:6,则S△ABD:S△CDB=$\frac{11}{25}$.
已知:AC平分∠DAB,∠DAB+∠DCB=180°,若CE:CB=5:6,则S△ABD:S△CDB=$\frac{11}{25}$. 抛物线y=ax2+b+c的部分图象如图所示,则当y<0时,x的取值范围是x<-1或x>3.
抛物线y=ax2+b+c的部分图象如图所示,则当y<0时,x的取值范围是x<-1或x>3.