题目内容
20.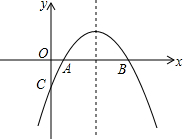 如图抛物线y=-x2+bx+c与x轴的两个交点别为A(1,0),B(3,0)
如图抛物线y=-x2+bx+c与x轴的两个交点别为A(1,0),B(3,0)(1)求这条抛物线所对应的函数关系式;
(2)设点P在该抛物线上滑动,若使△PAB的面积为1,这样的点P有几个?并求出满足P点的坐标;
(3)设抛物线交y轴于点C,在该抛物线对称轴上是否存在点M,使得△MAC的周长最小?若存在,求出点M的坐标;若不存在,请说明理由.
分析 (1)根据抛物线y=-x2+bx+c与x轴的两个交点别为A(1,0),B(3,0),由待定系数法即可得到这条抛物线所对应的函数关系式;
(2)根据(1)中得出的抛物线的解析式,可求得顶点的坐标,根据两点之间的距离公式能得出AB的长.△PAB中,AB的长为定值,那么可根据△PAB的面积求出P到AB的距离,即P点纵坐标的绝对值,然后将其代入抛物线的解析式中(分正负两个值)即可求出P点的坐标.
(3)本题的关键是找出M点的位置,已知B与A点关于抛物线的对称轴对称,因此只需连接BC,直线BC与对称轴的交点即为M点.可根据B、C两点的坐标先求出直线BC的解析式,然后联立抛物线对称轴的解析式即可求出M点的坐标.
解答 解:(1)∵抛物线y=-x2+bx+c与x轴的两个交点别为A(1,0),B(3,0),
∴$\left\{\begin{array}{l}{-1+b+c=0}\\{-9+3b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=3}\\{c=-3}\end{array}\right.$.
∴y=-x2-4x-3;
(2)符合条件的点P有三个.
y=-x2+4x-3=-(x-2)2+1,
则顶点为(2,1),
∵AB=2,S△PAB=1,
∴P点的纵坐标为±1,
当y=1时,P为抛物线顶点,
当y=-1时,-1=-(x-2)2+1,
解得x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$.
∴符合条件的坐标有(2,1),(2+$\sqrt{2}$,-1),(2-$\sqrt{2}$,-1);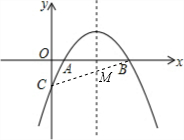 (3)存在,连结BC,BC与对称轴的交点为M,
(3)存在,连结BC,BC与对称轴的交点为M,
若在对称轴上另取一点M′,则M′C+M′A=M′C+M′B>BC,
则△MAC周长最小,
设过点B,C的直线的解析式y=kx-3,把B(3,0)代入可得3k-3=0,
解得k=1,
∴直线BC的解析式为y=x-3,
当x=2时,y=2-3=-1,
则M(2,-1).
点评 本题主要考查了二次函数综合题,涉及二次函数解析式的确定,图形面积的求法,函数图象的交点等知识;(3)题中能正确的找出M点的位置是解题的关键所在.

 如图为y=ax2+bx+c的图象,则( )
如图为y=ax2+bx+c的图象,则( )| A. | a>0,b<0 | B. | a>0,b>0 | C. | b<0,c<0 | D. | a<0,c<0 |
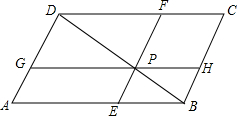 如图,在?ABCD中,P是对角线BD上的任意一点,过点P作EF∥BC,分别与AB,CD相交于点E,F;过点P再作GH∥AB,分别与AD,BC相交于点G,H,图中有几个平行四边形?其中哪几对平行四边形面积相等?为什么?
如图,在?ABCD中,P是对角线BD上的任意一点,过点P作EF∥BC,分别与AB,CD相交于点E,F;过点P再作GH∥AB,分别与AD,BC相交于点G,H,图中有几个平行四边形?其中哪几对平行四边形面积相等?为什么?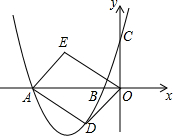 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(-4,0),B(-1,0)两点.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(-4,0),B(-1,0)两点.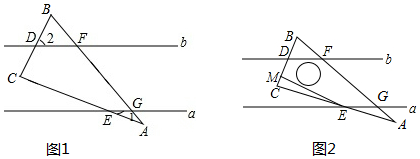
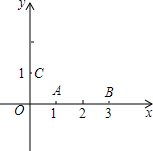 如图,已知点A(1,0)、B(3,0)、C(0,1).
如图,已知点A(1,0)、B(3,0)、C(0,1).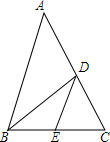 如图,在△ABC中,若$\frac{AB}{AD}$=$\frac{BC}{CD}$,AB=9,BC=6,DE∥AB,则△DCE的面积与四边形ABED的面积比是多少?
如图,在△ABC中,若$\frac{AB}{AD}$=$\frac{BC}{CD}$,AB=9,BC=6,DE∥AB,则△DCE的面积与四边形ABED的面积比是多少?