题目内容
2.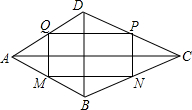 已知:如图,在四边形ABCD中,AB=AD,CB=CD,点M,N,N,P,Q分别是AB,BC,CD,DA的中点,求证:四边形MNPQ是矩形.
已知:如图,在四边形ABCD中,AB=AD,CB=CD,点M,N,N,P,Q分别是AB,BC,CD,DA的中点,求证:四边形MNPQ是矩形.
分析 首先设AC与BD交于点O,AC与QM交于点F,BD与PQ交于点E,由AB=AD,CB=CD,可得AC是BD的垂直平分线,由点M,N,N,P,Q分别是AB,BC,CD,DA的中点,根据三角形中位线的性质,易证得四边形OEQF是平行四边形,则可得∠MQP=∠AOD=90°,同理:∠QMN=∠MNP=90°,继而证得四边形MNPQ是矩形.
解答 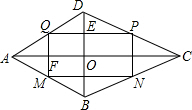 证明:如图,设AC与BD交于点O,AC与QM交于点F,BD与PQ交于点E,
证明:如图,设AC与BD交于点O,AC与QM交于点F,BD与PQ交于点E,
∵AB=AD,CB=CD,
∴点A与点C都在BD的垂直平分线上,
∴AC是BD的垂直平分线,即AC⊥BD,
∴∠AOD=90°,
∵点M,N,N,P,Q分别是AB,BC,CD,DA的中点,
∴MQ∥BD,PQ∥AC,
∴四边形OEQF是平行四边形,
∴∠MQP=∠AOD=90°,
同理:∠QMN=∠MNP=90°,
∴四边形MNPQ是矩形.
点评 此题考查了矩形的判定、三角形中位线的性质以及平行四边形的性质与判定.注意证得AC是BD的垂直平分线与四边形OEQF是平行四边形是解此题的关键.

练习册系列答案
相关题目
10.下表是两种类型的电话计费方式.
(1)某都市通用户某次主叫时间为3分钟25秒,求这次通话产生的费用;
(2)请根据下表(由环球通用户某月的电话清单整理),计算该用户这个月的费用:
(3)若某用户每月主叫与被叫的次数一样多,每次主叫与被叫的时间在1分钟以内,1到2分钟以内,2到3分钟以内,3到4分钟以内的次数之比为4:3:1:1.请根据他的通话次数确定选择什么类型的电话计费方式,才能使每月的费用最省?
| 类型 | 收费方式 |
| 都市通 | 月租费25元,被叫免费,主叫:3分钟以内,收费0.2元;超过3分钟的部分.每分钟0.1元,不足1分钟按1分钟计 |
| 环球通 | 月租费10元,主叫、被叫都按每分钟0.1元计费,不足1分钟按1分钟计 |
(2)请根据下表(由环球通用户某月的电话清单整理),计算该用户这个月的费用:
| 主叫 | 被叫 | |||||
| 通话时间长/分钟 | 2 | 3 | 4 | 3 | 4 | 5 |
| 次数 | 10 | 25 | 15 | 25 | 20 | 5 |
9. 如图为y=ax2+bx+c的图象,则( )
如图为y=ax2+bx+c的图象,则( )
 如图为y=ax2+bx+c的图象,则( )
如图为y=ax2+bx+c的图象,则( )| A. | a>0,b<0 | B. | a>0,b>0 | C. | b<0,c<0 | D. | a<0,c<0 |
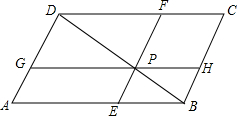 如图,在?ABCD中,P是对角线BD上的任意一点,过点P作EF∥BC,分别与AB,CD相交于点E,F;过点P再作GH∥AB,分别与AD,BC相交于点G,H,图中有几个平行四边形?其中哪几对平行四边形面积相等?为什么?
如图,在?ABCD中,P是对角线BD上的任意一点,过点P作EF∥BC,分别与AB,CD相交于点E,F;过点P再作GH∥AB,分别与AD,BC相交于点G,H,图中有几个平行四边形?其中哪几对平行四边形面积相等?为什么?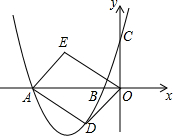 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(-4,0),B(-1,0)两点.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(-4,0),B(-1,0)两点.