题目内容
18.等腰△ABC底边BC=8cm,腰长AB=5cm,一动点P在底边上从点B开始向点C以1cm/秒的速度运动,当点P运动到PA与腰垂直的位置时,那么点P运动的时间为1.75或6.25 秒.分析 根据等腰三角形三线合一性质可得到BD的长,由勾股定理可求得AD的长,再分两种情况进行分析:①PA⊥AC②PA⊥AB,从而可得到运动的时间.
解答 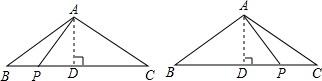 解:如图,作AD⊥BC,交BC于点D,
解:如图,作AD⊥BC,交BC于点D,
∵BC=8cm,
∴BD=CD=$\frac{1}{2}$BC=4cm,
∵AB=5cm,
∴AD=3cm,
分两种情况:当点P运动t秒后有PA⊥AC时,
∵AP2=PD2+AD2=PC2-AC2,
∴PD2+AD2=PC2-AC2,
∴PD2+32=(PD+4)2-52,
∴PD=2.25cm,
∴BP=4-2.25=1.75=t,
∴t=1.75秒,
当点P运动t秒后有PA⊥AB时,同理可证得PD=2.25,
∴BP=4+2.25=6.25=t,
∴t=6.25秒,
∴点P运动的时间为1.75秒或6.25秒.
故答案为:1.75或6.25.
点评 此题考查了等腰三角形的性质和勾股定理的运用,此题难度适中,解题的关键是分类讨论思想、方程思想与数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9. 如图为y=ax2+bx+c的图象,则( )
如图为y=ax2+bx+c的图象,则( )
 如图为y=ax2+bx+c的图象,则( )
如图为y=ax2+bx+c的图象,则( )| A. | a>0,b<0 | B. | a>0,b>0 | C. | b<0,c<0 | D. | a<0,c<0 |
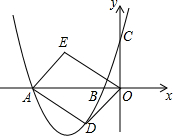 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(-4,0),B(-1,0)两点.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(-4,0),B(-1,0)两点.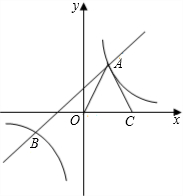 如图,反比例函数${y_1}=\frac{m}{x}$与一次函数y2=kx+b的图象交于两点A(1,3)、B(n,-1).
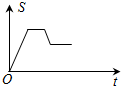
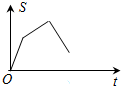
如图,反比例函数${y_1}=\frac{m}{x}$与一次函数y2=kx+b的图象交于两点A(1,3)、B(n,-1).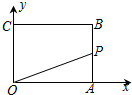 如图,已知矩形OABC,A(4,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
如图,已知矩形OABC,A(4,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )

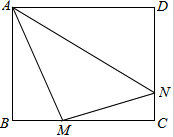 如图,正方形ABCD的边长为4,M,N分别是BC,CD上的两个动点,当点M在BC上运动时,保持AM和MN垂直.
如图,正方形ABCD的边长为4,M,N分别是BC,CD上的两个动点,当点M在BC上运动时,保持AM和MN垂直.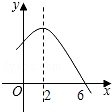 已知二次函数y=-x2+4x+m的部分图象如图所示,则关于x的一元二次方程-x2+4x+m=0的解为x1=-2,x2=6.
已知二次函数y=-x2+4x+m的部分图象如图所示,则关于x的一元二次方程-x2+4x+m=0的解为x1=-2,x2=6.