题目内容
19．△ABC中，∠C=90°，∠A的平分线交BC于点D，如果AB=8，CD=3，则△ABD的面积为（ ）| A． | 24 | B． | 12 | C． | 8 | D． | 6 |
分析 要求△ABD的面积，现有AB=8可作为三角形的底，只需求出该底上的高即可，需作DE⊥AB于E．根据角平分线的性质求得DE的长，即可求解．
解答 
解：作DE⊥AB于E．
∵AD平分∠BAC，DE⊥AB，DC⊥AC，
∴DE=CD=3，
∴△ABD的面积为$\frac{1}{2}$×3×8=12．
故选B．
点评 此题主要考查角平分线的性质；熟练运用角平分线的性质定理，是很重要的，作出并求出三角形AB边上的高时解答本题的关键．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
9．
如图为y=ax2+bx+c的图象，则（ ）
如图为y=ax2+bx+c的图象，则（ ）| A． | a＞0，b＜0 | B． | a＞0，b＞0 | C． | b＜0，c＜0 | D． | a＜0，c＜0 |
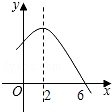已知二次函数y=-x2+4x+m的部分图象如图所示，则关于x的一元二次方程-x2+4x+m=0的解为x1=-2，x2=6．
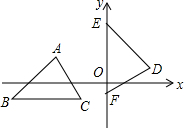如图，△ABC≌△DEF，其中A，B，C的对应顶点分别为D，E，F．若A点的坐标分别为（-5，3），B，C点的纵坐标都为-3，E，F点在y轴上，D点在第一象限，则D点的横坐标为6．
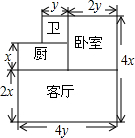如图是一所住宅的建筑平面图（图中长度单位：m）．