题目内容
10. 如图,直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.
如图,直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.(1)求证:直线FG是⊙O的切线;
(2)若FG=4,⊙O的半径为5,求四边形FGDE的面积.
分析 (1)利用角平分线的性质以及等腰三角形的性质得出∠OFC=∠FCG,进而得出∠GFC+∠OFC=90°,即可得出答案;
(2)首先得出四边形FGDH是矩形,进而利用勾股定理得出HO的长,进而得出答案.
解答 (1)证明:连接FO,
∵OF=OC,
∴∠OFC=∠OCF.
∵CF平分∠ACE,
∴∠FCG=∠FCE.
∴∠OFC=∠FCG.
∵CE是⊙O的直径,
∴∠EDG=90°,
又∵FG∥ED,
∴∠FGC=180°-∠EDG=90°,
∴∠GFC+∠FCG=90°
∴∠GFC+∠OFC=90°,
即∠GFO=90°,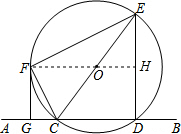
∴OF⊥GF,
又∵OF是⊙O半径,
∴FG与⊙O相切.
(2)解:延长FO,与ED交于点H,
由(1)可知∠HFG=∠FGD=∠GDH=90°,
∴四边形FGDH是矩形.
∴FH⊥ED,
∴HE=HD.
又∵四边形FGDH是矩形,FG=HD,
∴HE=FG=4.
∴ED=8.
∵在Rt△OHE中,∠OHE=90°,
∴OH=$\sqrt{O{E}^{2}-H{E}^{2}}$=3.
∴FH=FO+OH=5+3=8.
S四边形FGDH=$\frac{1}{2}$(FG+ED)•FH=$\frac{1}{2}$×(4+8)×8=48.
点评 此题主要考查了切线的判定以及矩形的判定与性质,得出HO的长是解题关键.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
20.2015年央视春晚微信摇一摇互动总量达110亿次,将110亿用科学记数法表示为( )
| A. | 110×108 | B. | 11×109 | C. | 1.1×1010 | D. | 1.1×1011 |
5. 如图是一几何体的三视图,这个几何体可能是( )
如图是一几何体的三视图,这个几何体可能是( )
 如图是一几何体的三视图,这个几何体可能是( )
如图是一几何体的三视图,这个几何体可能是( )| A. | 三棱柱 | B. | 三棱锥 | C. | 圆柱 | D. | 圆锥 |
2.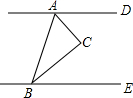 若AD∥BE,AC平分∠DAB,CB平分∠ABE,∠CBE=30°,则∠CAD的度数为( )
若AD∥BE,AC平分∠DAB,CB平分∠ABE,∠CBE=30°,则∠CAD的度数为( )
 若AD∥BE,AC平分∠DAB,CB平分∠ABE,∠CBE=30°,则∠CAD的度数为( )
若AD∥BE,AC平分∠DAB,CB平分∠ABE,∠CBE=30°,则∠CAD的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |

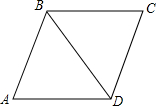 如图,在菱形ABCD中,∠BAC=30°,则∠B=120度.
如图,在菱形ABCD中,∠BAC=30°,则∠B=120度.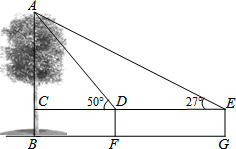 某数学兴趣小组用高为1.2米的测角仪测量小树AB的高度,如图,在距AB一定距离的F处测得小树顶部A的仰角为50°,沿BF方向行走3.5米到G处时,又测得小树顶部A的仰角为27°,求小树AB的高度.(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.5,sin50°=0.77,cos50°=0.64,tan50°=1.2)
某数学兴趣小组用高为1.2米的测角仪测量小树AB的高度,如图,在距AB一定距离的F处测得小树顶部A的仰角为50°,沿BF方向行走3.5米到G处时,又测得小树顶部A的仰角为27°,求小树AB的高度.(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.5,sin50°=0.77,cos50°=0.64,tan50°=1.2)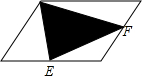 已知平行四边形的面积是128平方厘米,E、F分别是两条边上的中点,求阴影部分的面积.
已知平行四边形的面积是128平方厘米,E、F分别是两条边上的中点,求阴影部分的面积.