题目内容
19.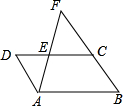 如图,已知在平行四边形ABCD中,点E是CD上一点,且DE=2,CE=3,射线AE与射线BC相交于点F;
如图,已知在平行四边形ABCD中,点E是CD上一点,且DE=2,CE=3,射线AE与射线BC相交于点F;(1)求$\frac{EF}{AF}$的值;
(2)如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,求向量$\overrightarrow{EF}$;(用向量$\overrightarrow a$、$\overrightarrow b$表示)
分析 (1)根据平行四边形的性质得出AB=5、AB∥EC,证△FEC∽△FAB得$\frac{EF}{AF}$=$\frac{EC}{AB}$=$\frac{3}{5}$;
(2)由△FEC∽△FAB得$\frac{EC}{AB}$=$\frac{FC}{FB}=\frac{EC}{AB}=\frac{3}{5}$,从而知FC=$\frac{3}{2}$BC,EC=$\frac{3}{5}$AB,再由平行四边形性质及向量可得$\overrightarrow{EC}$=$\frac{3}{5}$$\overrightarrow{AB}$=$\frac{3}{5}$$\overrightarrow{a}$,$\overrightarrow{FC}$=$\frac{3}{2}$$\overrightarrow{BC}$=$\frac{3}{2}$$\overrightarrow{b}$,最后根据向量的运算得出答案.
解答 解:(1)∵四边形ABCD是平行四边形,DE=2,CE=3,
∴AB=DC=DE+CE=5,且AB∥EC,
∴△FEC∽△FAB,
∴$\frac{EF}{AF}$=$\frac{EC}{AB}$=$\frac{3}{5}$;
(2)∵△FEC∽△FAB,
∴$\frac{EC}{AB}$=$\frac{FC}{FB}=\frac{EC}{AB}=\frac{3}{5}$,
∴FC=$\frac{3}{2}$BC,EC=$\frac{3}{5}$AB,
∵四边形ABCD是平行四边形,
∴AD∥BC,EC∥AB,
∴$\overrightarrow{AD}$=$\overrightarrow{BC}$=$\overrightarrow{b}$,
∴$\overrightarrow{EC}$=$\frac{3}{5}$$\overrightarrow{AB}$=$\frac{3}{5}$$\overrightarrow{a}$,$\overrightarrow{FC}$=$\frac{3}{2}$$\overrightarrow{BC}$=$\frac{3}{2}$$\overrightarrow{b}$,
则$\overrightarrow{EF}$=$\overrightarrow{EC}$+$\overrightarrow{CF}$=$\frac{3}{5}\overrightarrow{a}+\frac{3}{2}\overrightarrow{b}$.
点评 本题主要考查相似三角形的判定与性质、平行四边形的性质及向量的运算,熟练掌握相似三角形的判定与性质是解题的关键.

| A. | a2<b2 | B. | 2a<2b | C. | a+2<b+2 | D. | -a<-b |
| A. | y=2x2 | B. | y=2x-2 | C. | y=ax2 | D. | $y=\frac{a}{x^2}$ |
| A. | x2+y2+2x+2y | B. | x2+y2+2xy-2 | C. | x2-y2+4x+4y | D. | x2-y2+4y-4 |
| A. | y=2(x+3)2+3 | B. | y=2(x-3)2+3 | C. | y=2(x+3)2-1 | D. | y=2(x-3)2-1 |