题目内容
9.已知在Rt△ABC中,∠C=90°,∠A=α,BC=2,那么AB的长等于( )| A. | $\frac{2}{sinα}$ | B. | 2sinα | C. | $\frac{2}{cosα}$ | D. | 2cosα |
分析 根据锐角三角函数的定义得出sinA=$\frac{BC}{AB}$,代入求出即可.
解答 解:∵在Rt△ABC中,∠C=90°,∠A=α,BC=2,
∴sinA=$\frac{BC}{AB}$,
∴AB=$\frac{BC}{sinA}$=$\frac{2}{sinα}$,
故选A.
点评 本题考查了锐角三角函数的定义,能熟记锐角三角函数的定义是解此题的关键,注意:在Rt△ACB中,∠ACB=90°,则sinA=$\frac{BC}{AB}$,cosA=$\frac{AC}{AB}$,tanA=$\frac{BC}{AC}$.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
 如图,已知:AB为⊙O的直径,过A作弦AC、AD,并延长与过B的切线交于M、N,求证:∠MCN=∠MDN.
如图,已知:AB为⊙O的直径,过A作弦AC、AD,并延长与过B的切线交于M、N,求证:∠MCN=∠MDN.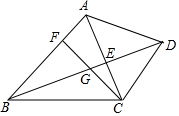 已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GE•GD.
已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GE•GD. 如图,在△ABC中,AB=AC,点D、E是边BC上的两个点,且BD=DE=EC,过点C作CF∥AB交AE延长线于点F,连接FD并延长与AB交于点G;
如图,在△ABC中,AB=AC,点D、E是边BC上的两个点,且BD=DE=EC,过点C作CF∥AB交AE延长线于点F,连接FD并延长与AB交于点G; 已知:如图,在△ABC中,点D,E分别在边AB,BC上,BA•BD=BC•BE
已知:如图,在△ABC中,点D,E分别在边AB,BC上,BA•BD=BC•BE