题目内容
2.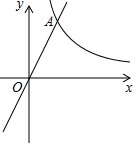 已知:如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.
已知:如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.(1)求平移后直线的表达式;
(2)求∠OBC的余切值.
分析 (1)根据点A在反比例函数图象上可求出点A的坐标,进而可求出正比例函数表达式,根据平移的性质可设直线BC的函数解析式为y=2x+b,根据点B的坐标利用待定系数法即可求出b值,此题得解;
(2)利用一次函数图象上点的坐标特征即可求出点C的坐标,从而得出OC的值,再根据余切的定义即可得出结论.
解答 解:(1)当x=2时,y=$\frac{8}{2}$=4,
∴点A的坐标为(2,4).
∵A(2,4)在y=kx(k≠0)的图象上,
∴4=2k,解得:k=2.
设直线BC的函数解析式为y=2x+b,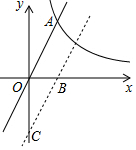
∵点B的坐标为(3,0),
∴0=2×3+b,解得:b=-6,
∴平移后直线的表达式y=2x-6.
(2)当x=0时,y=-6,
∴点C的坐标为(0,-6),
∴OC=6.
∴$cot∠OBC=\frac{OB}{OC}=\frac{3}{6}=\frac{1}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题、一次函数图象上点的坐标特征以及解直角三角形,根据点B的坐标利用待定系数法求出直线BC的解析式是解题的关键.

练习册系列答案
相关题目
10.已知a>b,下列关系式中一定正确的是( )
| A. | a2<b2 | B. | 2a<2b | C. | a+2<b+2 | D. | -a<-b |
7.在下列y关于x的函数中,一定是二次函数的是( )
| A. | y=2x2 | B. | y=2x-2 | C. | y=ax2 | D. | $y=\frac{a}{x^2}$ |
12.某运动队要从甲、乙、丙、丁四名运动员中选一名队员参加正式比赛,在选拔赛中,这四名运动员成绩的平均数与方差如下表所示:
若要根据选拔赛的成绩,选择一名成绩的平均数高且发挥稳定的队员参加正式比赛,则应选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数 | 8 | 9 | 9 | 8 |
| 方差 | 1 | 1 | 1.2 | 1.3 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
