题目内容
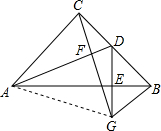 如图,在等腰直角三角形ABC中,∠ACB=90°,点D为BC的中点,DE⊥AB,垂足为点E,过点B作BG∥AC交DE的延长线于点G,连接CG,
如图,在等腰直角三角形ABC中,∠ACB=90°,点D为BC的中点,DE⊥AB,垂足为点E,过点B作BG∥AC交DE的延长线于点G,连接CG,(1)求证:△DBE≌△GBE;
(2)求证:AD⊥CF;
(3)连接AG,判断△ACG的形状,并说明理由.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)易证∠GBE=∠DBE=45°,即可证明△DBE≌△GBE;
(2)易证BG=BD,可得BG=CD,即可证明△ACD≌△CBG,可得∠BCG=∠CAD,即可求得∠CAD+∠ACF=90°,即可解题;
(3)易得DE=EG,即可证明△ADE≌△AGE,可得AD=AG,易得AD=CG,即可求得AG=CG,即可解题.
(2)易证BG=BD,可得BG=CD,即可证明△ACD≌△CBG,可得∠BCG=∠CAD,即可求得∠CAD+∠ACF=90°,即可解题;
(3)易得DE=EG,即可证明△ADE≌△AGE,可得AD=AG,易得AD=CG,即可求得AG=CG,即可解题.
解答:证明:(1)∵BG∥AC,∴∠GBC+∠ACB=180°,
∴∠GBC=90°,
∵∠ABC=45°,
∴∠GBE=∠DBE=45°,
∵在△DBE和△GBE中,
,
∴△DBE≌△GBE(ASA);
(2)∵△DBE≌△GBE,
∴BG=BD,
∵点D为BC的中点,
∴BD=CD,∴BG=CD,
∵在△ACD和△CBG中,
,
∴△ACD≌△CBG,(SAS)
∴∠BCG=∠CAD,
∵∠BCG+∠ACF=90°,
∴∠CAD+∠ACF=90°,
∴AD⊥CF;
(3)∵△DBE≌△GBE,
∴DE=EG,
∵在△ADE和△AGE中,
,
∴△ADE≌△AGE,(SAS)
∴AD=AG,
∵△ACD≌△CBG,
∴AD=CG,
∴AG=CG,
∴△ACG为等腰三角形.
∴∠GBC=90°,
∵∠ABC=45°,
∴∠GBE=∠DBE=45°,
∵在△DBE和△GBE中,
|
∴△DBE≌△GBE(ASA);
(2)∵△DBE≌△GBE,
∴BG=BD,
∵点D为BC的中点,
∴BD=CD,∴BG=CD,
∵在△ACD和△CBG中,
|
∴△ACD≌△CBG,(SAS)
∴∠BCG=∠CAD,
∵∠BCG+∠ACF=90°,
∴∠CAD+∠ACF=90°,
∴AD⊥CF;
(3)∵△DBE≌△GBE,
∴DE=EG,
∵在△ADE和△AGE中,
|
∴△ADE≌△AGE,(SAS)
∴AD=AG,
∵△ACD≌△CBG,
∴AD=CG,
∴AG=CG,
∴△ACG为等腰三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,考查了等腰三角形的判定,本题中求证△DBE≌△GBE、△ACD≌△CBG和△ADE≌△AGE是解题的关键.

练习册系列答案
相关题目
不等式
-
≥1的正整数解是( )
| x-1 |
| 6 |
| x-3 |
| 2 |
| A、0 | B、1 | C、0和1 | D、0或1 |
据省统计局公布信息:今年“十一”黄金周游客,西安再创游客人数和旅游收入新高.7天我市共接待游客630.01万人次,同比增长33.3%;游客总收入29.12亿元人民币.同比增长29.47%,其中数据29.12亿元用科学记数法表示是( )
| A、2.92×10元 |
| B、2.912×109元 |
| C、2.912×108元 |
| D、2.912×107元 |
 如图,AB是⊙O的直径,PA,PC是⊙O的两条切线,连接CA.若AB=4,PC=6,则AC的长为( )
如图,AB是⊙O的直径,PA,PC是⊙O的两条切线,连接CA.若AB=4,PC=6,则AC的长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 有一圆柱,在圆柱下底的A点处有一只蚂蚁,它想吃到上底面与A点相对的B点处的食物,沿圆柱侧面爬行,如圆柱高为1dm,底面圆半径为2dm,则爬行的最短路程是
有一圆柱,在圆柱下底的A点处有一只蚂蚁,它想吃到上底面与A点相对的B点处的食物,沿圆柱侧面爬行,如圆柱高为1dm,底面圆半径为2dm,则爬行的最短路程是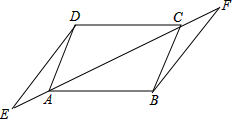 如图,AD∥BC,AE=CF,AD=BC,点E,F在直线AC上,试猜想线段DE与BF有何关系,并说明你的猜想.
如图,AD∥BC,AE=CF,AD=BC,点E,F在直线AC上,试猜想线段DE与BF有何关系,并说明你的猜想.