题目内容
 有一圆柱,在圆柱下底的A点处有一只蚂蚁,它想吃到上底面与A点相对的B点处的食物,沿圆柱侧面爬行,如圆柱高为1dm,底面圆半径为2dm,则爬行的最短路程是
有一圆柱,在圆柱下底的A点处有一只蚂蚁,它想吃到上底面与A点相对的B点处的食物,沿圆柱侧面爬行,如圆柱高为1dm,底面圆半径为2dm,则爬行的最短路程是考点:平面展开-最短路径问题
专题:
分析:要想求得最短路程,首先要把A和B展开到一个平面内.根据两点之间,线段最短求出蚂蚁爬行的最短路程.
解答: 解:如图所示,
解:如图所示,
∵圆柱高为1dm,底面圆半径为2dm,
∴BD=1dm,AD=2πdm,
∴AB=
≈
=
(dm).
故答案为:
dm.
 解:如图所示,
解:如图所示,∵圆柱高为1dm,底面圆半径为2dm,
∴BD=1dm,AD=2πdm,
∴AB=
| 4π2+1 |
| 4×9+1 |
| 37 |
故答案为:
| 37 |
点评:本题考查的是平面展开-最短路径问题,此类问题应先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
把直线y=x+2向上平移n个单位后,与直线y=-2x+5的交点在第二象限,则n的取值范围是( )
| A、1<n<7 | B、n<5 |
| C、2<n<5 | D、n>3 |
x的3倍减去2的差不大于0,列出不等式为( )
| A、3x-2≤0 |
| B、3x-2≥0 |
| C、3x-2<0 |
| D、3x-2>0 |
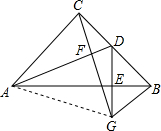 如图,在等腰直角三角形ABC中,∠ACB=90°,点D为BC的中点,DE⊥AB,垂足为点E,过点B作BG∥AC交DE的延长线于点G,连接CG,
如图,在等腰直角三角形ABC中,∠ACB=90°,点D为BC的中点,DE⊥AB,垂足为点E,过点B作BG∥AC交DE的延长线于点G,连接CG,