题目内容
已知关于x的一元二次方程x2+2x+2k-4=0有两个不相等的整数根，若k为正整数，则k= ．
考点：根的判别式
专题：
分析：根据方程有两个不相等的实数根，得到根的判别式的值大于0列出关于k的不等式，求出不等式的解集得到k的范围，找出k范围中的正整数解确定出k的值，经检验即可得到满足题意k的值．
解答：解：根据题意得：△=4-4（2k-4）=20-8k＞0，
解得：k＜
，
∵k为正整数，得到k=1或2，
利用求根公式表示出方程的解为x=-1±
，
∵方程的解为整数，
∴5-2k为完全平方数，
∴k的值为2．
故答案为2．
解得：k＜
| 5 |
| 2 |
∵k为正整数，得到k=1或2，
利用求根公式表示出方程的解为x=-1±
| 5-2k |
∵方程的解为整数，
∴5-2k为完全平方数，
∴k的值为2．
故答案为2．
点评：此题考查了根的判别式，一元二次方程的解，以及公式法解一元二次方程，弄清题意是解本题的关键．
练习册系列答案
相关题目
如图，矩形ABCD是供一辆机动车停放的车位示意图，已知BC=2m，CD=5，∠DCF=30°，请你计算车位所占的宽度EF约为多少米？（把直线y=x+2向上平移n个单位后，与直线y=-2x+5的交点在第二象限，则n的取值范围是（ ）
| A、1＜n＜7 | B、n＜5 |
| C、2＜n＜5 | D、n＞3 |
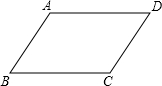如图，请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并予以证明．（写出一种即可）x的3倍减去2的差不大于0，列出不等式为（ ）
| A、3x-2≤0 |
| B、3x-2≥0 |
| C、3x-2＜0 |
| D、3x-2＞0 |
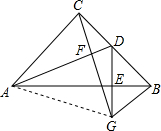如图，在等腰直角三角形ABC中，∠ACB=90°，点D为BC的中点，DE⊥AB，垂足为点E，过点B作BG∥AC交DE的延长线于点G，连接CG，