题目内容
若关于x的一元二次方程x2+2x+k=0无实数根,则k值可以是( )
| A、-5 | B、0 | C、1 | D、3 |
考点:根的判别式
专题:
分析:若关于x的一元二次方程x2+2x+k=0没有实数根,则△=b2-4ac<0,列出关于k的不等式,求得k的取值范围即可选择.
解答:解:∵关于x的一元二次方程x2+2x+k=0没有实数根,
∴∴△=b2-4ac<0,
即22-4×1×k<0,
解这个不等式得:k>1,
∴只有3符合要求.
故选:D.
∴∴△=b2-4ac<0,
即22-4×1×k<0,
解这个不等式得:k>1,
∴只有3符合要求.
故选:D.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
已知x=4是方程式ax-2=a+10的解,则a值为( )
| A、2 | B、-3 | C、4 | D、-4 |
一元二次方程x2-2=0的根是( )
A、x=
| ||||
| B、x=2或x=-2 | ||||
| C、x=-2 | ||||
| D、x=2 |
一元二次方程x2-3x+1=0的两个根分别是x1,x2,则x12+x22的值是( )
| A、3 | B、7 | C、-9 | D、11 |
已知3是关于x的方程5x-a=3的解,则a的值是( )
| A、-14 | B、12 |
| C、14 | D、-13 |
将方程
-
=1去分母,得到6x-3-2x-2=6,错在( )
| 2x-1 |
| 2 |
| x-1 |
| 3 |
| A、最简公分母找错 |
| B、去分母时,漏乘3项 |
| C、去分母时,分子部分没有加括号 |
| D、去分母时,各项所乘的数不同 |
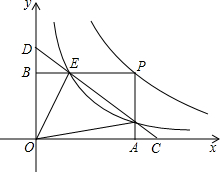 如图,点P是反比例函数y=
如图,点P是反比例函数y= 如图,⊙O是△ABC的内切圆,点D、E分别为边AC、BC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )
如图,⊙O是△ABC的内切圆,点D、E分别为边AC、BC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )