Question

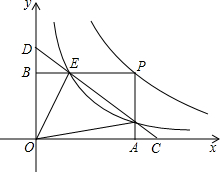如图，点P是反比例函数y=

m

x

（x＞0）图象上的一点，矩形OAPB的顶点A、B分别在x轴与y轴上，且边PB、PA分别交反比例函数y=

k

x

（x＞0）的图象于E、F两点，直线EF交x轴于点C，连接OE、OF．求证：DE=CF．

Answer 1

考点：反比例函数综合题

专题：综合题

分析：作EH⊥OA于H，FG⊥OB于G，如图，根据反比例函数图象上点的坐标特征可设P（a，

m

a

），则E的纵坐标为

m

a

，F点的横坐标为a，于是可表示出E（a，

k

a

），F（

ak

m

，

m

a

），再证明△DBE∽△DGF得到

DE

DF

=

BE

GF

=

k

m

，根据比例的性质得

DE

EF

=

k

m-k

①，再证明△CAF∽△CHE得到

CF

CE

=

AF

EH

=

k

m

，根据比例的性质得

CF

EF

=

k

m-k

②，然后由①②即可得到DE=CF．

解答：解：作EH⊥OA于H，FG⊥OB于G，如图，
设P（a，

m

a

），则E的纵坐标为

m

a

，F点的横坐标为a，
∵E、F点在反比例函数y=

k

x

（x＞0）的图象上，
∴E（a，

k

a

），F（

ak

m

，

m

a

），
∵BE∥GF，
∴△DBE∽△DGF，
∴

DE

DF

=

BE

GF

=

ak m

a

=

k

m

，
∴

DE

EF

=

k

m-k

①，
∵AF∥EH，
∴△CAF∽△CHE，
∴

CF

CE

=

AF

EH

=

k a

m a

=

k

m

，
∴

CF

EF

=

k

m-k

②，
由①②得

DE

EF

=

CF

EF

，
∴DE=CF．

点评：本题考查了反比例函数的综合题：熟练掌握反比例函数图象上点的坐标特征和矩形的性质；会使用相似三角形的判定与性质解决线段之间的关系；会运用比例的性质进行计算．