题目内容
将方程
-
=1去分母，得到6x-3-2x-2=6，错在（ ）
| 2x-1 |
| 2 |
| x-1 |
| 3 |
| A、最简公分母找错 |
| B、去分母时，漏乘3项 |
| C、去分母时，分子部分没有加括号 |
| D、去分母时，各项所乘的数不同 |
考点：解一元一次方程
专题：计算题
分析：方程两边乘以6得到结果，即可做出判断．
解答：解：将方程
-
=1去分母，得：3（2x-1）-2（x-1）=6，
去括号得：6x-3-2x+2=6，
错误在去分母时，分子部分没有加括号，
故选C
| 2x-1 |
| 2 |
| x-1 |
| 3 |
去括号得：6x-3-2x+2=6，
错误在去分母时，分子部分没有加括号，
故选C
点评：此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，把未知数系数化为1，求出解．
练习册系列答案
相关题目
若点A的坐标（x，y）满足条件（x-3）2+|y+2|=0，则点A关于y轴的对称点的坐标是（ ）
| A、（3，2） |
| B、（-3，2） |
| C、（3，-2） |
| D、（-3，-2） |
关于x的一元二次方程x2-mx+（m-2）=0（m为任意实数）的根的情况是（ ）
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、无实数根 |
| D、有无实数根，无法判断 |
若关于x的一元二次方程x2+2x+k=0无实数根，则k值可以是（ ）
| A、-5 | B、0 | C、1 | D、3 |
若关于x的一元二次方程ax2-2x+1=0有两个实数根，则实数a的取值范围是（ ）
| A、a≤1且a≠0 |
| B、a＜1且a≠0 |
| C、a≤1 |
| D、a＜1 |
下列方程中，以x=
为解的是（ ）
| 1 |
| 2 |
| A、2x-4=0 |
| B、2x-1=x+1 |
| C、3-4x=2x-3 |
| D、2x-1=0 |
方程2（x-1）=
的解是（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
数m、n在数轴上的位置如图所示，则化简|m+n|-m的结果是（ ）| A、2m+n | B、2m | C、m | D、n |
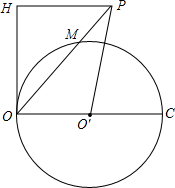如图，点P为圆O′外一点，OC为圆O′的直径，PO=OC，PO交圆O′于M，OH为圆O′的切线，且PH垂直于OH，若OH=2PM，求tan∠OPO′的值．