题目内容
 如图,⊙O是△ABC的内切圆,点D、E分别为边AC、BC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )
如图,⊙O是△ABC的内切圆,点D、E分别为边AC、BC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )| A、7 | B、8 | C、9 | D、16 |
考点:切线长定理
专题:
分析:根据切线长定理,可得BI=BG,CI=CH,DG=DF,EF=EH,则C△ADE=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=C△ABC-(BG+EH+BC),据此即可求解.
解答: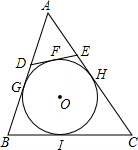 解:∵AB、AC、BC、DE都和⊙O相切,
解:∵AB、AC、BC、DE都和⊙O相切,
∴BI=BG,CI=CH,DG=DF,EF=EH.
∴BG+CH=BI+CI=BC=9,
∴C△ADE=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=C△ABC-(BG+EH+BC)=25-2×9=7.
故选A.
 解:∵AB、AC、BC、DE都和⊙O相切,
解:∵AB、AC、BC、DE都和⊙O相切,∴BI=BG,CI=CH,DG=DF,EF=EH.
∴BG+CH=BI+CI=BC=9,
∴C△ADE=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=C△ABC-(BG+EH+BC)=25-2×9=7.
故选A.
点评:本题考查了切线长定理,理解定理,找出图形中存在的相等的线段是关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
若关于x的一元二次方程x2+2x+k=0无实数根,则k值可以是( )
| A、-5 | B、0 | C、1 | D、3 |
 数m、n在数轴上的位置如图所示,则化简|m+n|-m的结果是( )
数m、n在数轴上的位置如图所示,则化简|m+n|-m的结果是( )| A、2m+n | B、2m | C、m | D、n |
 已知,如图,在平面直角坐标系内,点A的坐标为(0,12),经过原点的直线l,与经过点A的直线12相交于点B,点B的坐标为(9,3).
已知,如图,在平面直角坐标系内,点A的坐标为(0,12),经过原点的直线l,与经过点A的直线12相交于点B,点B的坐标为(9,3).
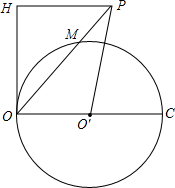 如图,点P为圆O′外一点,OC为圆O′的直径,PO=OC,PO交圆O′于M,OH为圆O′的切线,且PH垂直于OH,若OH=2PM,求tan∠OPO′的值.
如图,点P为圆O′外一点,OC为圆O′的直径,PO=OC,PO交圆O′于M,OH为圆O′的切线,且PH垂直于OH,若OH=2PM,求tan∠OPO′的值. 如图,已知AB是⊙O的直径,点C在⊙O上,点D是BC的中点,若AC=10cm,则OD=
如图,已知AB是⊙O的直径,点C在⊙O上,点D是BC的中点,若AC=10cm,则OD=