题目内容
一元二次方程x2-2=0的根是( )
A、x=
| ||||
| B、x=2或x=-2 | ||||
| C、x=-2 | ||||
| D、x=2 |
考点:解一元二次方程-直接开平方法
专题:计算题
分析:方程移项后,利用平方根定义开方即可求出解.
解答:解:方程移项得:x2=2,
开方得:x=
或x=-
,
故选A
开方得:x=
| 2 |
| 2 |
故选A
点评:此题考查了解一元二次方程-直接开平方法,熟练掌握平方根的定义是解本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
若点A的坐标(x,y)满足条件(x-3)2+|y+2|=0,则点A关于y轴的对称点的坐标是( )
| A、(3,2) |
| B、(-3,2) |
| C、(3,-2) |
| D、(-3,-2) |
某超市一月份营业额为10万元,一至三月份总营业额为50万元,若平均每月增长率为x,则所列方程为( )
| A、10(1+x)2=50 |
| B、10+10×2x=50 |
| C、10+10×3x=50 |
| D、10+10(1+x)+10(1+x)2=50 |
解方程
-
=1,去分母正确的是( )
| x-3 |
| 4 |
| 1+2x |
| 8 |
| A、2(x-3)-(1+2x)=8 |
| B、2(x-3)-1+2x=8 |
| C、2(x-3)-(1+2x)=1 |
| D、2(x-3)-1+2x=1 |
关于x的一元二次方程x2-mx+(m-2)=0(m为任意实数)的根的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、无实数根 |
| D、有无实数根,无法判断 |
若关于x的一元二次方程x2+2x+k=0无实数根,则k值可以是( )
| A、-5 | B、0 | C、1 | D、3 |
 数m、n在数轴上的位置如图所示,则化简|m+n|-m的结果是( )
数m、n在数轴上的位置如图所示,则化简|m+n|-m的结果是( )| A、2m+n | B、2m | C、m | D、n |
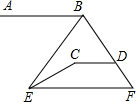 如图,AB∥CD∥EF,若∠ABE=48°,∠ECD=148°.求∠BEC的度数.
如图,AB∥CD∥EF,若∠ABE=48°,∠ECD=148°.求∠BEC的度数.