题目内容
10.若点P(-m,1-2m)关于原点对称的点在第一象限,那么m的取值范围是m>$\frac{1}{2}$.分析 先判断出点P在第三象限,再根据第三象限内点的横坐标与纵坐标都是负数列不等式组求解即可.
解答 解:∵点P(-m,1-2m)关于原点对称的点在第一象限,
∴点P在第三象限,
∴$\left\{\begin{array}{l}{-m<0①}\\{1-2m<0②}\end{array}\right.$,
解不等式①得,m>0,
解不等式②得,m>$\frac{1}{2}$,
所以,不等式组的解集是m>$\frac{1}{2}$,
即m的取值范围是m>$\frac{1}{2}$.
故答案为:m>$\frac{1}{2}$.
点评 本题考查了关于原点对称的点的坐标,解一元一次不等式组,两点关于原点对称,则两点的横、纵坐标都是互为相反数.

练习册系列答案
相关题目
10.6月是某地暴雨多发季节,6月10日,某水库的水位从9:00开始持续上涨,下表记录了最近4小时内5个时间点的水位高度.
设水位上长时间为x小时,水位高度为y米.
(1)若水位按照以上上涨规律,当日14:00时,水位高度为6.5米,此时x=5小时;
(2)试写出一个符合表中数据的y关于x的函数关系式;
(3)该水库的最高警戒水位是7米,据统计,这祌上涨规律还会持续3个多小时,当时13:00时,驻地距离水库72千米远的武警官兵接到水库管理员的报警求救电话,防汛指挥部要求武警官兵必须在水库水位到警戒水位武警官兵接到电话后,立即从驻地出发,则他们赶往水库的速度需要什么条件?
| 时刻 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 |
| 水位高度(米) | 5 | 5.3 | 5.6 | 5.9 | 6.2 |
(1)若水位按照以上上涨规律,当日14:00时,水位高度为6.5米,此时x=5小时;
(2)试写出一个符合表中数据的y关于x的函数关系式;
(3)该水库的最高警戒水位是7米,据统计,这祌上涨规律还会持续3个多小时,当时13:00时,驻地距离水库72千米远的武警官兵接到水库管理员的报警求救电话,防汛指挥部要求武警官兵必须在水库水位到警戒水位武警官兵接到电话后,立即从驻地出发,则他们赶往水库的速度需要什么条件?
7.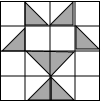 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
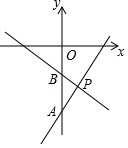 如图,一次函数y1=ax-9(a≠0)与y2=bx-3(b≠0)的图象交于点P,与y轴分别交于点A,B,若S△ABP=12,则关于x的不等式bx+6>ax的解集是x<4.
如图,一次函数y1=ax-9(a≠0)与y2=bx-3(b≠0)的图象交于点P,与y轴分别交于点A,B,若S△ABP=12,则关于x的不等式bx+6>ax的解集是x<4. 如图,正方形ABCD和正方形DEFG的顶点A在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B、C和边EF的中点M,若正方形ABCD的边长为2,则正方形DEFG的面积为$\frac{32}{9}$.
如图,正方形ABCD和正方形DEFG的顶点A在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B、C和边EF的中点M,若正方形ABCD的边长为2,则正方形DEFG的面积为$\frac{32}{9}$.