题目内容
9.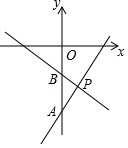 如图,一次函数y1=ax-9(a≠0)与y2=bx-3(b≠0)的图象交于点P,与y轴分别交于点A,B,若S△ABP=12,则关于x的不等式bx+6>ax的解集是x<4.
如图,一次函数y1=ax-9(a≠0)与y2=bx-3(b≠0)的图象交于点P,与y轴分别交于点A,B,若S△ABP=12,则关于x的不等式bx+6>ax的解集是x<4.
分析 先利用直线解析式写出A、B点的坐标,再利用三角形面积公式求出P点的横坐标,然后利用函数图象,写出直线y=bx-3在直线y=ax-9上方所对应的自变量的范围即可.
解答 解:当x=0时,y1=ax-9=-9,则A(0,-9),
当x=0时,y2=bx-3=-3,则B(0,-3),
所以AB=6,
设P点的横坐标为x,
则$\frac{1}{2}$x•6=12,解得x=4,
当x<4时,bx-3>ax-9,
所以bx+6>ax的解集为x<4.
故答案为x<4.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
20. 如图,一直线与两坐标轴的正半轴分别交于A、B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20,则该直线的函数表达式是( )
如图,一直线与两坐标轴的正半轴分别交于A、B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20,则该直线的函数表达式是( )
 如图,一直线与两坐标轴的正半轴分别交于A、B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20,则该直线的函数表达式是( )
如图,一直线与两坐标轴的正半轴分别交于A、B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20,则该直线的函数表达式是( )| A. | y=x+10 | B. | y=-x+10 | C. | y=x+20 | D. | y=-x+20 |
17.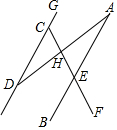 如图,下列条件不能判定AB∥CD的是( )
如图,下列条件不能判定AB∥CD的是( )
 如图,下列条件不能判定AB∥CD的是( )
如图,下列条件不能判定AB∥CD的是( )| A. | ∠BAD=∠ADG | B. | ∠GCE=∠AEF | C. | ∠GDH+∠DHF=180° | D. | ∠FEB+∠GCE=180° |
4.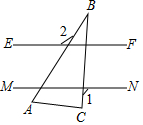 把含有30°的直角三角板(∠ABC=30°)如图放置,若EF∥MN,∠1=100°,则∠2的度数为( )
把含有30°的直角三角板(∠ABC=30°)如图放置,若EF∥MN,∠1=100°,则∠2的度数为( )
 把含有30°的直角三角板(∠ABC=30°)如图放置,若EF∥MN,∠1=100°,则∠2的度数为( )
把含有30°的直角三角板(∠ABC=30°)如图放置,若EF∥MN,∠1=100°,则∠2的度数为( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
18.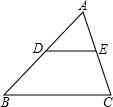 如图,点D,E分別在三角形ABC的边AB,AC上,若DE∥BC,∠B=50°,则∠ADE=( )
如图,点D,E分別在三角形ABC的边AB,AC上,若DE∥BC,∠B=50°,则∠ADE=( )
 如图,点D,E分別在三角形ABC的边AB,AC上,若DE∥BC,∠B=50°,则∠ADE=( )
如图,点D,E分別在三角形ABC的边AB,AC上,若DE∥BC,∠B=50°,则∠ADE=( )| A. | 30° | B. | 40° | C. | 50° | D. | 130° |
 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1m),却踩伤了花草.
如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1m),却踩伤了花草.