题目内容
8．已知（x2+mx+n）（x+2）的结果中不含x2项和x项，求m、n的值．分析 先根据多项式乘以多项式法则展开，合并同类项，得出方程，求出即可．
解答 解：（x2+mx+n）（x+2）
=x3+2x2+mx2+2mx+nx+2n
=x3+（2+m）x2+（2m+n）x+2n，
∵（x2+mx+n）（x+2）的结果中不含x2项和x项，
∴2+m=0，2m+n=0，
解得：m=-2，n=4．
点评 本题考查了多项式乘以多项式，能得出关于m、n的方程是解此题的关键．
练习册系列答案
相关题目
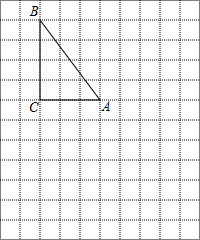在右边网格图中，每个小正方形的边长均为1个单位长度，△ABC为直角三角形，∠C=90°，AC=3，BC=4．
如图，在△ABC中，∠A=90，BD是角平分线，若AD=m，BC=n，则△BDC的面积为$\frac{1}{2}$mn．
抛物线C1：y=a（x+1）（x-3a）（a＞0）与x轴交于A，B两点（A在B的左侧），与y轴交于点C（0，-3）