题目内容
13.(1)($\sqrt{45}$+$\sqrt{27}$)-($\sqrt{\frac{4}{3}}$+$\sqrt{125}$)(2)(1-$\sqrt{3}$+$\sqrt{2}$)(1+$\sqrt{3}$-$\sqrt{2}$)
分析 (1)先化简题目中的二次根式,然后去括号,合并同类项即可解答本题;
(2)根据平方差公式和完全平方公式可以解答本题.
解答 解:(1)($\sqrt{45}$+$\sqrt{27}$)-($\sqrt{\frac{4}{3}}$+$\sqrt{125}$)
=$(3\sqrt{5}+3\sqrt{3})-(\frac{2\sqrt{3}}{3}+5\sqrt{5})$
=$3\sqrt{5}+3\sqrt{3}-\frac{2\sqrt{3}}{3}-5\sqrt{5}$
=-2$\sqrt{5}$$+\frac{7\sqrt{3}}{3}$;
(2)(1-$\sqrt{3}$+$\sqrt{2}$)(1+$\sqrt{3}$-$\sqrt{2}$)
=$[1-(\sqrt{3}-\sqrt{2})][1+(\sqrt{3}-\sqrt{2})]$
=1-$(\sqrt{3}-\sqrt{2})^{2}$
=1-3+2$\sqrt{6}$-2
=-4+2$\sqrt{6}$.
点评 本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 对角线互相垂直且相等的四边形是正方形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 有两条边相等的平行四边形是菱形 | |
| D. | 三个角是直角的四边形是矩形 |
3.下列运算中,正确的是( )
| A. | 2x+2y=2xy | B. | (xy)2÷$\frac{1}{xy}$=(xy)3 | C. | (x2y3)2=x4y5 | D. | 2xy-3yx=xy |
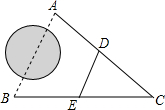 如图,A,B两地无法直接测量距离,现在地面上选一点C,连接CA,CB,分别取CA,CB的中点D,E,若测得DE的长为30m,那么A,B两地间的距离是60m.
如图,A,B两地无法直接测量距离,现在地面上选一点C,连接CA,CB,分别取CA,CB的中点D,E,若测得DE的长为30m,那么A,B两地间的距离是60m.
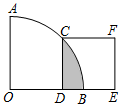 如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2时,阴影部分的面积为π-2.
如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2时,阴影部分的面积为π-2.