题目内容
 已知如图,I是△ABC的内心,以内切圆的半径为边长的正方形IDEF、EFHG放置于△ABC内,D、E、H、G都在三角形的边上,则tanC的值是 ( )
已知如图,I是△ABC的内心,以内切圆的半径为边长的正方形IDEF、EFHG放置于△ABC内,D、E、H、G都在三角形的边上,则tanC的值是 ( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:三角形的内切圆与内心
专题:
分析:如图,作辅助线;证明IG=2IF=2λ,得到∠IGM=30°;证明∠IGM=∠C=30°,即可解决问题.
解答: 解:如图,过点I作IM⊥AC于点M;
解:如图,过点I作IM⊥AC于点M;
∵I是△ABC的内心,四边形DEIF是正方形,
∴ID=IM(设为λ);
∵IG=2IF=2λ,
∴∠IGM=30°;
∵IG∥BC,
∴∠IGM=∠C=30°,
∴tanC的值是
.
故选D.
 解:如图,过点I作IM⊥AC于点M;
解:如图,过点I作IM⊥AC于点M;∵I是△ABC的内心,四边形DEIF是正方形,
∴ID=IM(设为λ);
∵IG=2IF=2λ,
∴∠IGM=30°;
∵IG∥BC,
∴∠IGM=∠C=30°,
∴tanC的值是
| ||
| 3 |
故选D.
点评:该题主要考查了三角形内切圆的性质及其应用问题;解题的关键是作辅助线,灵活运用有关定理来分析判断.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
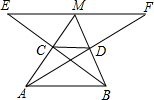 如图,在梯形ABCD中,AB∥CD,AB=a,CD=b,两腰的延长线交于点M,过M作DC的平行线,分别交BC、AD的延长线于点E、F,则EF等于( )
如图,在梯形ABCD中,AB∥CD,AB=a,CD=b,两腰的延长线交于点M,过M作DC的平行线,分别交BC、AD的延长线于点E、F,则EF等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知AB∥CD,GH是直线,∠1+∠2=180°,问CD与EF是否平行?为什么?
如图,已知AB∥CD,GH是直线,∠1+∠2=180°,问CD与EF是否平行?为什么? 一个圆锥形漏斗,某同学用三角波测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为
一个圆锥形漏斗,某同学用三角波测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为