题目内容
20.(1)计算:(29$\frac{2}{3}$)2=880$\frac{1}{9}$;(2)计算:1992×2012=3999.
分析 (1)把29$\frac{2}{3}$变形为30-$\frac{1}{3}$,然后利用完全平方公式计算;
(2)把199化为(200-1),把201化为(200+1),然后根据平方差公式计算.
解答 解:(1)原式=(30-$\frac{1}{3}$)2=302-2×30×$\frac{1}{3}$+($\frac{1}{3}$)2=900-20+$\frac{1}{9}$=880$\frac{1}{9}$;
(2)原式=(200-1)(200+1)=2002-12=40000-1=3999.
故答案为880$\frac{1}{9}$;3999.
点评 本题考查完全平方公式:(a±b)2=a2±2ab+b2.也考查了平方差公式.本题的关键是构建完全平方公式和平方差公式的形式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.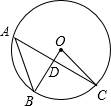 如图,已知A,B,C三点在⊙O上,AC⊥BO于O,∠B=55°,则∠BOC的度数为( )
如图,已知A,B,C三点在⊙O上,AC⊥BO于O,∠B=55°,则∠BOC的度数为( )
 如图,已知A,B,C三点在⊙O上,AC⊥BO于O,∠B=55°,则∠BOC的度数为( )
如图,已知A,B,C三点在⊙O上,AC⊥BO于O,∠B=55°,则∠BOC的度数为( )| A. | 45° | B. | 35° | C. | 70° | D. | 80° |
15.一个三角形的两边长分别为4和7,则此三角形的第三边的取值范围是( )
| A. | 3<x<11 | B. | 4<x<7 | C. | -3<x<11 | D. | x>3 |
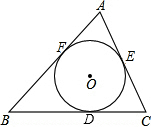 △ABC的内切圆⊙O的半径为3,点D、E、F为切点.△ABC的周长为18,求△ABC的面积.
△ABC的内切圆⊙O的半径为3,点D、E、F为切点.△ABC的周长为18,求△ABC的面积.