题目内容
9.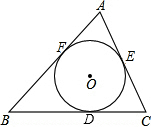 △ABC的内切圆⊙O的半径为3,点D、E、F为切点.△ABC的周长为18,求△ABC的面积.
△ABC的内切圆⊙O的半径为3,点D、E、F为切点.△ABC的周长为18,求△ABC的面积.
分析 连接OA、OB、OC,OD、OE、OF,则OD=OE=OF=3,由三角形的面积得出S△ABC=S△AOB+S△OBC+S△OAC=$\frac{1}{2}$×3×(AB+BC+AC),即可得出结果.
解答 解:连接OA、OB、OC,OD、OE、OF,如图所示: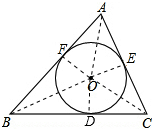
则OD⊥BC,OE⊥AC,OF⊥AB,OD=OE=OF=3,
∴S△ABC=S△AOB+S△OBC+S△OAC
=$\frac{1}{2}$×AB×3+$\frac{1}{2}$×BC×3+$\frac{1}{2}$×AC×3
=$\frac{1}{2}$×3×(AB+BC+AC)
=$\frac{1}{2}$×3×18
=27.
点评 本题考查了三角形的内切圆与内心、切线的性质、三角形面积的计算方法;熟练掌握三角形内心的性质,由分割法计算三角形的面积得出三角形的周长是解决问题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
19.某汽车行驶时油箱中余油量Q(千克)与行驶时间t(小时)的关系如下:
(1)写出用时间t表示余油量Q的代数式:Q=40-4t;
(2)当t=$\frac{7}{4}$时,余油量Q的值是33;
(3)根据所列代数式回答,汽车行驶之前油箱中有油多少千克?
(4)邮箱中原有的汽油可供汽车行驶多少小时?
| 行驶时间t/h | 1 | 2 | 3 | 4 | 5 |
| 余油量Q/kg | 40-4 | 40-8 | 40-12 | 40-16 | 40-20 |
(2)当t=$\frac{7}{4}$时,余油量Q的值是33;
(3)根据所列代数式回答,汽车行驶之前油箱中有油多少千克?
(4)邮箱中原有的汽油可供汽车行驶多少小时?

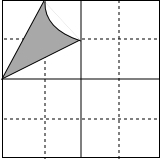 如图,已知网格中每个小正方形的边长为都是1,图中的阴影部分图案是一条以格点为圆心,以1为半径的圆弧和两条线段围成.
如图,已知网格中每个小正方形的边长为都是1,图中的阴影部分图案是一条以格点为圆心,以1为半径的圆弧和两条线段围成.