题目内容
10.将一张长方形的纸对折,如图所示,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么如果对折五次,可以得到31条折痕.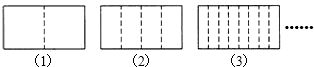
分析 观察图形,对折1次,是2-1=1条折痕,对折2次22-1=3条折痕,对折3次23-1=7条折痕,对折4次24-1=15条折痕,…,据此可得,对折n次是2n-1条折痕,据此即可解答问题.
解答 解:对折1次,折痕为1条,1=21-1,
对折2次,折痕为3条,3=22-1,
对折3次,折痕为7条,7=23-1,
…,
依此类推,对折n次,折痕为2n-1条,
所以,当n=5时,25-1=32-1=31.
故答案为:31.
点评 此题考查图形的变化规律,找出图形的变化规律,得出数字的运算方法,利用规律解决问题.

练习册系列答案
相关题目
15.“十一”国庆期间,俄罗斯特技飞行队在黄山湖公园特技表演,其中一架飞机起飞后的高度变化如表:
(1)此时这架飞机比起飞点高了多少千米?
(2)如果飞机每上升或下降1千米需消耗2升燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?
| 高度变化 | 记作 |
| 上升4.4km | 4.4km |
| 下降3.2km | -3.2km |
| 上升1.1km | +1.1km |
| 下降1.5km | -1.5km |
(2)如果飞机每上升或下降1千米需消耗2升燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?
2.十位上的数字是m,个位上的数字比十位上的数字大4的两位数是( )
| A. | 11m+4 | B. | m(m+4) | C. | 11m+40 | D. | 2m+4 |
19.某汽车行驶时油箱中余油量Q(千克)与行驶时间t(小时)的关系如下:
(1)写出用时间t表示余油量Q的代数式:Q=40-4t;
(2)当t=$\frac{7}{4}$时,余油量Q的值是33;
(3)根据所列代数式回答,汽车行驶之前油箱中有油多少千克?
(4)邮箱中原有的汽油可供汽车行驶多少小时?
| 行驶时间t/h | 1 | 2 | 3 | 4 | 5 |
| 余油量Q/kg | 40-4 | 40-8 | 40-12 | 40-16 | 40-20 |
(2)当t=$\frac{7}{4}$时,余油量Q的值是33;
(3)根据所列代数式回答,汽车行驶之前油箱中有油多少千克?
(4)邮箱中原有的汽油可供汽车行驶多少小时?
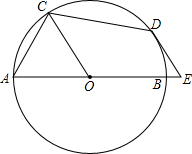 如图,在⊙O中,AB是直径,CD是⊙O上的点,E为AB延长线上一点,连接OC,CD,DE,满足∠OCD=45°且OC∥DE.
如图,在⊙O中,AB是直径,CD是⊙O上的点,E为AB延长线上一点,连接OC,CD,DE,满足∠OCD=45°且OC∥DE. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6.求以AB为直径的半圆的面积.
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6.求以AB为直径的半圆的面积.