题目内容
 如图,等腰△ABC中,AB=AC=5,∠BAC=45°,以BC为直角边,以B为直角顶点向三角形外作等腰直角△BCD,则AD的长为
如图,等腰△ABC中,AB=AC=5,∠BAC=45°,以BC为直角边,以B为直角顶点向三角形外作等腰直角△BCD,则AD的长为考点:全等三角形的判定与性质,勾股定理,等腰直角三角形
专题:常规题型
分析:过C、D分别作CE、DF分别垂直AB直线,即可证明△CBE≌△BDF,即可得DF=BE,BF=CE,在Rt△ACE中根据勾股定理即可求得AD的长.
解答: 解:过C作CE垂直于线段AB,过D作DF垂直于线段AB的延长线于F点,
解:过C作CE垂直于线段AB,过D作DF垂直于线段AB的延长线于F点,
∵∠CBE+∠BCE=90°,∠DBF+∠CBE=90°,
∴∠BCE=∠DBF,
在△BCE和△DBF中,
,
∴△BCE≌△DBF(AAS),
∴DF=BE,BF=CE,
∵在Rt△ACE中,CE=AC•sin45°=
,BE=5-
,
∴DF=5-
,AF=AB+BF=5+
,
∴在RT△ADF中,根据勾股定理计算AD=
=5
.
故答案为5
.
 解:过C作CE垂直于线段AB,过D作DF垂直于线段AB的延长线于F点,
解:过C作CE垂直于线段AB,过D作DF垂直于线段AB的延长线于F点,∵∠CBE+∠BCE=90°,∠DBF+∠CBE=90°,
∴∠BCE=∠DBF,
在△BCE和△DBF中,
|
∴△BCE≌△DBF(AAS),
∴DF=BE,BF=CE,
∵在Rt△ACE中,CE=AC•sin45°=
5
| ||
| 2 |
5
| ||
| 2 |
∴DF=5-
5
| ||
| 2 |
5
| ||
| 2 |
∴在RT△ADF中,根据勾股定理计算AD=
| DF2+AF2 |
| 3 |
故答案为5
| 3 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了勾股定理的运用,本题中求证△BCE≌△DBF是解题的关键.

练习册系列答案
相关题目
某厂一月份生产某机器300台,计划二、三月份共生产980台.设二三月份每月的平均增长率为x,根据题意列出的方程是( )
| A、300(1+x)2=980 |
| B、300(1+x)+300(1+x)2=980 |
| C、300(1-x)2=980 |
| D、300+300(1+x)+300(1+x)2=980 |
方程x2-2=0的解为( )
| A、2 | ||||
B、
| ||||
| C、2与-2 | ||||
D、
|
 如图,有甲、乙两栋楼房,已知两楼之间的距离是24m,有一身高为1.80m的人站在甲楼楼顶距楼边1.80m处向下观看,正好看到乙楼的楼底,求甲楼的高度.
如图,有甲、乙两栋楼房,已知两楼之间的距离是24m,有一身高为1.80m的人站在甲楼楼顶距楼边1.80m处向下观看,正好看到乙楼的楼底,求甲楼的高度.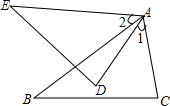 已知:如图,AB=AE,∠1=∠2,AD=AC
已知:如图,AB=AE,∠1=∠2,AD=AC