题目内容
10.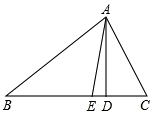 如图,AD,AE分别是△ABC的高和角平分线.
如图,AD,AE分别是△ABC的高和角平分线.(1)已知∠B=40°,∠C=60°,求∠DAE的度数;
(2)设∠B=α,∠C=β(α<β).请用含α、β的代数式表示∠DAE.∠DAE=$\frac{1}{2}$(β-α).并证明.
分析 (1)根据三角形的内角和等于180°列式求出∠BAC,再根据角平分线的定义求出∠BAE,根据直角三角形两锐角互余求出∠BAD,然后根据∠DAE=∠BAD-∠BAE代入数据计算即可得解;
(2)根据三角形的内角和等于180°列式表示出∠BAC,再根据角平分线的定义求出∠BAE,根据直角三角形两锐角互余求出∠BAD,然后根据∠DAE=∠BAD-∠BAE整理即可得解.
解答 解:(1)∵∠B=40°,∠C=60°,
∴∠BAC=180°-∠B-∠C=180°-40°-60°=80°,
∵AE是角平分线,
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×80°=40°,
∵AD是高,
∴∠BAD=90°-∠B=90°-40°=50°,
∴∠DAE=∠BAD-∠BAE=50°-40°=10°;
(2)$\frac{1}{2}$(β-α).
∵∠B=α,∠C=β(α<β),
∴∠BAC=180°-(α+β),
∵AE是角平分线,
∴∠BAE=$\frac{1}{2}$∠BAC=90°-$\frac{1}{2}$(α+β),
∵AD是高,
∴∠BAD=90°-∠B=90°-α,
∴∠DAE=∠BAD-∠BAE=90°-α-[90°-$\frac{1}{2}$(α+β)]=$\frac{1}{2}$(β-α).
故答案为:$\frac{1}{2}$(β-α).
点评 本题考查了三角形的内角和定理,角平分线的定义,直角三角形两锐角互余的性质,熟练掌握定理与概念并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
20.下列各数中,比-2小的数是( )
| A. | 0 | B. | -1 | C. | -3 | D. | 1 |
5.若一对相似三角形的相似比为1:3,则这对三角形的面积比为( )
| A. | 1:3 | B. | 3:1 | C. | 1:9 | D. | 1:$\sqrt{3}$ |
15.关于x的一元二次方程x2-kx-1=0的根的情况是( )
| A. | 没有实数根 | B. | 有一个实数根 | ||
| C. | 有两个相等的实数根 | D. | 有两个不相等的实数根 |
2.$\frac{1}{2}$的相反数是( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
19.下列各式中能用平方差公式因式分解的是( )
| A. | -x2y2 | B. | x2+y2 | C. | x2-y2 | D. | x-y |
 已知线段a,c的长如图所示,求作Rt△ABC,使斜边AB=c,直角边BC=a.要求用尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑.
已知线段a,c的长如图所示,求作Rt△ABC,使斜边AB=c,直角边BC=a.要求用尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑. 6块同样大小的长方形复合地板刚好拼成一个大长方形,如图,你能算出每块复合地板的长和宽吗?
6块同样大小的长方形复合地板刚好拼成一个大长方形,如图,你能算出每块复合地板的长和宽吗?


