题目内容
18. 6块同样大小的长方形复合地板刚好拼成一个大长方形,如图,你能算出每块复合地板的长和宽吗?
6块同样大小的长方形复合地板刚好拼成一个大长方形,如图,你能算出每块复合地板的长和宽吗?
分析 设每块复合地板的长为xcm,宽为ycm,根据图形中大长方形的长和宽即可得出关于x、y的二元一次方程组,解之即可得出结论.
解答 解:设每块复合地板的长为xcm,宽为ycm,
根据题意得:$\left\{\begin{array}{l}{x+y=30}\\{2x=x+2y}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=20}\\{y=10}\end{array}\right.$.
答:每块复合地板的长为20cm,宽为10cm.
点评 本题考查了二元一次方程组的应用,根据图形找出小长方形长与宽之间的关系是解题的关键.

练习册系列答案
相关题目
8. 如图,AB 为⊙O 的切线,切点为 B,连接 AO 与⊙O 交与点 C,BD 为⊙O 的直径,连接 CD,若∠A=30°,OA=2,则图中阴影部分的面积为( )
如图,AB 为⊙O 的切线,切点为 B,连接 AO 与⊙O 交与点 C,BD 为⊙O 的直径,连接 CD,若∠A=30°,OA=2,则图中阴影部分的面积为( )
 如图,AB 为⊙O 的切线,切点为 B,连接 AO 与⊙O 交与点 C,BD 为⊙O 的直径,连接 CD,若∠A=30°,OA=2,则图中阴影部分的面积为( )
如图,AB 为⊙O 的切线,切点为 B,连接 AO 与⊙O 交与点 C,BD 为⊙O 的直径,连接 CD,若∠A=30°,OA=2,则图中阴影部分的面积为( )| A. | $\frac{π}{3}-\frac{{\sqrt{3}}}{4}$ | B. | $\frac{4π}{3}-2\sqrt{3}$ | C. | $π-\sqrt{3}$ | D. | $\frac{4}{3}π-\sqrt{3}$ |
3.下列各点位于函数y=x2-x+2的图象上的是( )
| A. | (1,2) | B. | (-1,2) | C. | (0,1) | D. | (1,0) |
8.将抛物线y=x2先向右平移1个单位长度,再向下平移2个单位长度可得抛物线( )
| A. | y=(x-1)2-2 | B. | y=(x+1)2-2 | C. | y=(x-1)2+2 | D. | y=(x+1)2+2 |
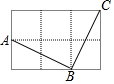 在由6个大小相同的小正方形组成的方格中;如图,A、B、C是三个格点(即小正方形的顶点).判断AB与BC的关系,并说明理由.
在由6个大小相同的小正方形组成的方格中;如图,A、B、C是三个格点(即小正方形的顶点).判断AB与BC的关系,并说明理由.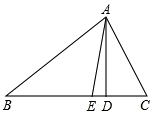 如图,AD,AE分别是△ABC的高和角平分线.
如图,AD,AE分别是△ABC的高和角平分线.