题目内容
15.关于x的一元二次方程x2-kx-1=0的根的情况是( )| A. | 没有实数根 | B. | 有一个实数根 | ||
| C. | 有两个相等的实数根 | D. | 有两个不相等的实数根 |
分析 先计算判别式的值得到△=k2+4,从而可判断△>0,则根据判别式的意义可判断方程根的情况.
解答 解:∵△=(-k)2-4×(-1)=k2+4>0,
∴方程有两个不相等的两个实数根.
故选D.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
3.下列各点位于函数y=x2-x+2的图象上的是( )
| A. | (1,2) | B. | (-1,2) | C. | (0,1) | D. | (1,0) |
20.2016年天猫双11落下帷幕,总成交额最终定格在120700000000元,是8年来成交额首次突破1000亿大关,数据120700000000元用科学记数法表示为( )
| A. | 12.07×1010 | B. | 1.207×1011 | C. | 1.207×1012 | D. | 1.207×1012 |
4.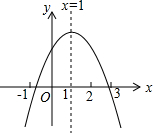 已知二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④c<4b;⑤a+b<k(ka+b)(k为常数,且k≠1).其中正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④c<4b;⑤a+b<k(ka+b)(k为常数,且k≠1).其中正确的结论有( )
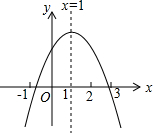 已知二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④c<4b;⑤a+b<k(ka+b)(k为常数,且k≠1).其中正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④c<4b;⑤a+b<k(ka+b)(k为常数,且k≠1).其中正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
5.能说明命题“若x(x+1)(x-2)=0,则x=0”是假命题的反例是( )
| A. | x=0 | B. | x=-2 | C. | x=1 | D. | x=-1 |
 (1)在如图所示的方格纸中,经过线段AB外一点C,画线段AB的垂线CH(垂足为H)和平行线EF.(画出的线请用铅笔描粗描黑)
(1)在如图所示的方格纸中,经过线段AB外一点C,画线段AB的垂线CH(垂足为H)和平行线EF.(画出的线请用铅笔描粗描黑)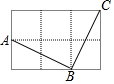 在由6个大小相同的小正方形组成的方格中;如图,A、B、C是三个格点(即小正方形的顶点).判断AB与BC的关系,并说明理由.
在由6个大小相同的小正方形组成的方格中;如图,A、B、C是三个格点(即小正方形的顶点).判断AB与BC的关系,并说明理由.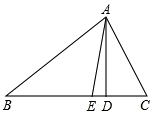 如图,AD,AE分别是△ABC的高和角平分线.
如图,AD,AE分别是△ABC的高和角平分线.