题目内容
19.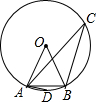 如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=$\frac{1}{9}$πcm2;②${l_{\widehat{AB}}}=\frac{2}{9}πcm$;③∠ACB=20°;④∠ADB=140°.错误的有( )
如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=$\frac{1}{9}$πcm2;②${l_{\widehat{AB}}}=\frac{2}{9}πcm$;③∠ACB=20°;④∠ADB=140°.错误的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 由正九边形的性质求出中心角的度数,再由扇形面积公式和弧长公式、圆周角定理以及圆内接四边形的性质即可得出①②③正确,④错误,即可得出结果.
解答 解:∵AB为⊙O内接正九边形的一边,
∴∠AOB=$\frac{360°}{9}$=40°,
∴S扇形AOB=$\frac{40π×{1}^{2}}{360}$=$\frac{1}{9}$π(cm2),$\widehat{AB}$的长=$\frac{40π×1}{180}$=$\frac{2}{9}$π(cm);∠ACB=$\frac{1}{2}$∠AOB=20°;
∴①②③正确;∠ADB=180°-20°=160°;
∴④错误;错误的有1个,
故选:B.
点评 本题考查了正九边形的性质、扇形面积公式和弧长公式、圆周角定理以及圆内接四边形的性质;求出正九边形的性质是解决问题的关键.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
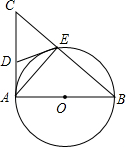 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E,连接AE.
如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E,连接AE.