题目内容
13.三元一次方程组$\left\{\begin{array}{l}{x+y=3}\\{y+z=4}\\{x+z=5}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=3}\end{array}\right.$.分析 先将三元一次方程转化为二元一次方程组,再转化为一元一次方程,即可解答本题.
解答 解:$\left\{\begin{array}{l}{x+y=3}&{①}\\{y+z=4}&{②}\\{x+z=5}&{③}\end{array}\right.$
①-②,得
x-z=-1④
③+④,得
x=2,
将x=2代入①,得y=1,
将x=2代入③,得z=3,
故元方程组的解是,$\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=3}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=3}\end{array}\right.$.
点评 本题考查解三元一次方程组,解题的关键是运用消元的思想将方程由三元最终转化为一元一次方程解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.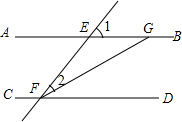 如图,AB∥CD,∠1=70°,FG平分∠EFD,则∠2的度数是( )
如图,AB∥CD,∠1=70°,FG平分∠EFD,则∠2的度数是( )
 如图,AB∥CD,∠1=70°,FG平分∠EFD,则∠2的度数是( )
如图,AB∥CD,∠1=70°,FG平分∠EFD,则∠2的度数是( )| A. | 30° | B. | 35° | C. | 40° | D. | 70° |
1.为调查某班学生每天使用零花钱的情况,张华随机调查了30名同学,结果如表:
则这30名同学每天使用的零花钱的众数和中位数分别是( )
| 每天使用零花钱(单位:元) | 1 | 2 | 3 | 4 | 5 |
| 人数 | 2 | 5 | 8 | 9 | 6 |
| A. | 4,3 | B. | 4,3.5 | C. | 3.5,3.5 | D. | 3.5,4 |
17.人工智能AlphaGo因在人机大战中大胜韩国围棋手李世石九段而声名显赫.它具有自我对弈学习能力,决战前已做了两千万局的训练(等同于一个人近千年的训练量).此处“两千万”用科学记数法表示为( )
| A. | 0.2×107 | B. | 2×107 | C. | 0.2×108 | D. | 2×108 |
 如图,已知正比例函数y=kx经过点P.
如图,已知正比例函数y=kx经过点P.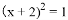 B.
B. 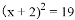
 D.
D.