题目内容
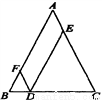
20. 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,则大楼AB的高度约为( )(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,则大楼AB的高度约为( )(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)| A. | 30.6 | B. | 32.1 | C. | 37.9 | D. | 39.4 |
分析 延长AB交DC于H,作EG⊥AB于G,则GH=DE=15米,EG=DH,设BH=x米,则CH=$\sqrt{3}$x米,在Rt△BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6$\sqrt{3}$米,得出BG、EG的长度,证明△AEG是等腰直角三角形,得出AG=EG=6$\sqrt{3}$+20(米),即可得出大楼AB的高度.
解答 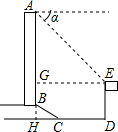 解:延长AB交DC于H,作EG⊥AB于G,如图所示:
解:延长AB交DC于H,作EG⊥AB于G,如图所示:
则GH=DE=15米,EG=DH,
∵梯坎坡度i=1:$\sqrt{3}$,
∴BH:CH=1:$\sqrt{3}$,
设BH=x米,则CH=$\sqrt{3}$x米,
在Rt△BCH中,BC=12米,
由勾股定理得:x2+($\sqrt{3}$x)2=122,
解得:x=6,∴BH=6米,CH=6$\sqrt{3}$米,
∴BG=GH-BH=15-6=9(米),EG=DH=CH+CD=6$\sqrt{3}$+20(米),
∵∠α=45°,
∴∠EAG=90°-45°=45°,
∴△AEG是等腰直角三角形,
∴AG=EG=6$\sqrt{3}$+20(米),
∴AB=AG+BG=6$\sqrt{3}$+20+9≈39.4(米);
故选:D.
点评 本题考查了解直角三角形的应用-坡度、俯角问题;通过作辅助线运用勾股定理求出BH,得出EG是解决问题的关键.

练习册系列答案
相关题目
11.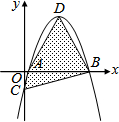 如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
 如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
8.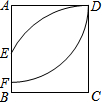 如图,以矩形ABCD的A为圆心,AD长为半径画弧,交AB于F点;再以C为圆心,CD长为半径画弧,交AB于E点.若AD=5,CD=$\frac{17}{3}$,则EF的长度为何?( )
如图,以矩形ABCD的A为圆心,AD长为半径画弧,交AB于F点;再以C为圆心,CD长为半径画弧,交AB于E点.若AD=5,CD=$\frac{17}{3}$,则EF的长度为何?( )
 如图,以矩形ABCD的A为圆心,AD长为半径画弧,交AB于F点;再以C为圆心,CD长为半径画弧,交AB于E点.若AD=5,CD=$\frac{17}{3}$,则EF的长度为何?( )
如图,以矩形ABCD的A为圆心,AD长为半径画弧,交AB于F点;再以C为圆心,CD长为半径画弧,交AB于E点.若AD=5,CD=$\frac{17}{3}$,则EF的长度为何?( )| A. | 2 | B. | 3 | C. | $\frac{2}{3}$ | D. | $\frac{7}{3}$ |
15.下列调查中,最适合采用全面调查(普查)的是( )
| A. | 对重庆市居民日平均用水量的调查 | |
| B. | 对一批LED节能灯使用寿命的调查 | |
| C. | 对重庆新闻频道“天天630”栏目收视率的调查 | |
| D. | 对某校九年级(1)班同学的身高情况的调查 |
12.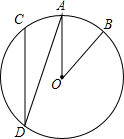 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )| A. | 40° | B. | 30° | C. | 20° | D. | 15° |
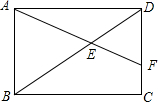 如图,矩形ABCD中,AB=$\sqrt{3}$,BC=$\sqrt{6}$,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于点F,则$\frac{CF}{CD}$=$\frac{1}{3}$.
如图,矩形ABCD中,AB=$\sqrt{3}$,BC=$\sqrt{6}$,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于点F,则$\frac{CF}{CD}$=$\frac{1}{3}$.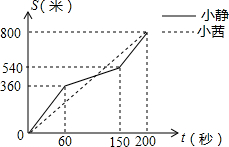 为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第120秒.
为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第120秒.