题目内容
如图,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是( )
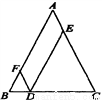
A. 5 B. 10 C. 20 D. 15
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
暑假作业海燕出版社系列答案题目内容
如图,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是( )
A. 5 B. 10 C. 20 D. 15
暑假作业海燕出版社系列答案
如图所示，某办公大楼正前方有一根高度是15米的旗杆ED，从办公楼顶端A测得旗杆顶端E的俯角α是45°，旗杆底端D到大楼前梯坎底边的距离DC是20米，梯坎坡长BC是12米，梯坎坡度i=1：$\sqrt{3}$，则大楼AB的高度约为（ ）（精确到0.1米，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，$\sqrt{6}$≈2.45）
，则BC的长为( )
＋1 B. 
＋1
数n都可以进行这样的分【解析】
，例如12可以分解成1×12,2×6或3×4，因为12-1＞6-2＞4-3，所有3×4是最佳分解，所以F（12）=
.
意一个完全平方数m，总有F（m）=1.
的运算结果应在哪两个连续自然数之间( )