Question

10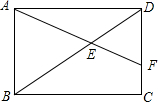．如图，矩形ABCD中，AB=$\sqrt{3}$，BC=$\sqrt{6}$，点E在对角线BD上，且BE=1.8，连接AE并延长交DC于点F，则$\frac{CF}{CD}$=$\frac{1}{3}$．

Answer 1

分析 根据勾股定理求出BD，得到DE的长，根据相似三角形的性质得到比例式，代入计算即可求出DF的长，求出CF，计算即可．

解答 解：∵四边形ABCD是矩形，
∴∠BAD=90°，又AB=$\sqrt{3}$，BC=$\sqrt{6}$，
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=3，
∵BE=1.8，
∴DE=3-1.8=1.2，
∵AB∥CD，
∴$\frac{DF}{AB}$=$\frac{DE}{BE}$，即$\frac{DF}{\sqrt{3}}$=$\frac{1.2}{1.8}$，
解得，DF=$\frac{2\sqrt{3}}{3}$，
则CF=CD-DF=$\frac{\sqrt{3}}{3}$，
∴$\frac{CF}{CD}$=$\frac{\frac{\sqrt{3}}{3}}{\sqrt{3}}$=$\frac{1}{3}$，
故答案为：$\frac{1}{3}$．

点评 本题考查的是矩形的性质、相似三角形的判定和性质，掌握矩形的性质定理和相似三角形的判定定理、性质定理是解题的关键．