题目内容
10．当m为何值时，分式方程$\frac{2m}{x-2}+m=\frac{x-1}{2-x}$无解？分析 分式方程去分母转化为整式方程，根据分式方程无解得到最简公分母为0求出x的值，代入整式方程即可求出m的值，还要注意整式方程无解的情形．
解答 解：方程两边同时乘以x-2得：2m+m（x-2）=-（x-1）
去括号得：2m+mx-2m=-x+1，
移项得：mx+x=1，
∵分式方程无解，
∴x-2=0，
即x=2，
把x=2代入mx+x=1得：2m+2=1，
解得：m=$-\frac{1}{2}$．
又m=-1时，方程无解，
综上，m=-1或-$\frac{1}{2}$
点评 此题考查了分式方程的解，解决本题的关键是明确分式方程无解即为最简公分母为0，注意一题多解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
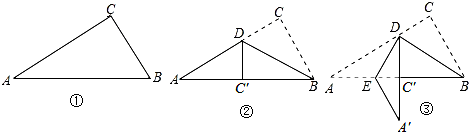
20．如图①是一个直角三角形纸片，∠A=30°，BC=4cm，将其折叠，使点C落在斜边上的点C′处，折痕为BD，如图②，再将②沿DE折叠．使点A落在DC′的延长线上的点A′处，如图③，则折痕DE的长为（ ）
| A． | $2\sqrt{2}$cm | B． | $2\sqrt{3}$cm | C． | $\frac{8}{3}$cm | D． | 3cm |
18．
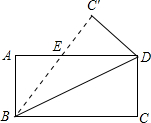如图，将长方形纸片ABCD沿对角线BD折叠，使点C落在C′处，BC′交AD于E．若∠DBC=22.5°，则在不添加任何辅助线的情况下，图中45°的角（虚线也视为角的边）有（ ）
如图，将长方形纸片ABCD沿对角线BD折叠，使点C落在C′处，BC′交AD于E．若∠DBC=22.5°，则在不添加任何辅助线的情况下，图中45°的角（虚线也视为角的边）有（ ）| A． | 3个 | B． | 4个 | C． | 5个 | D． | 6个 |
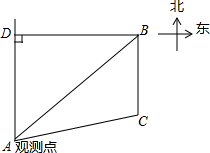已知B村庄位于A观测点北偏东53.2°方向，且其到A观测点正北方向的距离BD的长为24km，一辆摩托车从B村庄以60km/h的速度沿如图所示的BC方向航行，15min后达到C处，现测得C处位于A观测点北偏东79.8°方向，求此摩托车与A观测点之间的距离AC的长（精确到0.1km）．（参考数据：sin53.2°≈0.80，cos53.2°≈0.60，sin79.8°≈0.98，cos79.8°≈0.18，tan26.6°≈0.50，$\sqrt{2}$≈1.41，$\sqrt{5}$≈2.24．
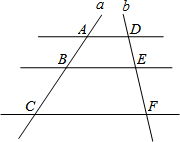如图，AD∥BE∥CF，直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F，若AB=2，AC=6，DE=1.5，则DF的长为（ ）
2．
某校八年级全体男同学参加了跳绳比赛，从中随机抽取某班男同学的跳绳成绩，制作了如下频数分布表：
根据上面统计信息，解答下列问题：
（1）不全频数分布直方图．
（2）班级准备对跳绳成绩优秀的男同学进行奖励，奖励人数占班级男同学的20%，该班张辉同学的成绩为140个，通过计算判断张辉能否获得奖励．
（3）八年级共有200名男同学，若规定男同学的跳绳成绩在120个以上（含120个）为合格，估计该校八年级男同学成绩合格的人数．
某校八年级全体男同学参加了跳绳比赛，从中随机抽取某班男同学的跳绳成绩，制作了如下频数分布表：| 组别 | 99.5-109.5 | 109.5-119.5 | 119.5-129.5 | 129.5-139.5 | 139.5-149.5 | 149.5-159.5 |
| 频数 | 2 | 4 | 8 | 7 | 3 | 1 |
（1）不全频数分布直方图．
（2）班级准备对跳绳成绩优秀的男同学进行奖励，奖励人数占班级男同学的20%，该班张辉同学的成绩为140个，通过计算判断张辉能否获得奖励．
（3）八年级共有200名男同学，若规定男同学的跳绳成绩在120个以上（含120个）为合格，估计该校八年级男同学成绩合格的人数．