题目内容
17. 如图,已知Rt△ABC,∠ACB=90°,
如图,已知Rt△ABC,∠ACB=90°,(1)根据下列语句作图并保留作图痕迹;作Rt△ABC的外接圆⊙O,过点A作⊙O的切线PA与AC的垂直平分线交于点P;并写出 过点A作⊙O的切线PA的作图依据;
(2)连接PC,求证:PC是⊙O的切线;
(3)已知PA=AC=$\sqrt{3}$,求线段PA、PC与弧AC围成的图形的面积.
分析 (1)利用直角三角形外接圆的性质,可得斜边中点为点O,以O为圆心,OA为半径作⊙O,然后根据切线的判定定理作出过点A的⊙O的切线PA;
(2)连结OC,利用切线的性质与判定,得出∠OAC+∠CAP=∠OCA+∠PCA=90°,即可得出答案;
(3)根据(2)中所求,可以得出△PAC是等边三角形,进而得出r=1,∠AOP=60°,∠AOC=120°,即可求出所求图形的面积.
解答 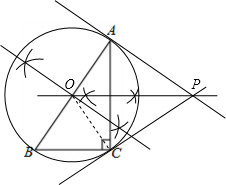 (1)解:如图所示:
(1)解:如图所示:
作图依据:经过半径的外端,并且垂直于这条半径的直线是圆的切线;
(2)证明:连结OC.
∵点P、O在AC垂直平分线上,
∴PA=PC,AO=CO,
∴∠PAC=∠PCA,∠OAC=∠OCA,
∵PA是⊙O的切线,
∴∠OAP=90°,
∴∠OAC+∠CAP=∠OCA+∠PCA=90°,
∴OC⊥PC,
∴PC是⊙O的切线;
(3)解:∵PA,PC都是⊙O的切线,
∴PA=PC,
∵PA=AC=$\sqrt{3}$,
∴PA=AC=PC,
∴△PAC是等边三角形,
∴∠PAC=60°,
∴∠OAC=30°,
∴r=1,∠AOP=60°,∠AOC=120°,
∴S四边形AOCP=$\frac{1}{2}$×1×$\sqrt{3}$×2=$\sqrt{3}$,
S扇形AOC=$\frac{1}{3}$π,
∴线段PA、PC与弧AC围成的图形的面积为$\sqrt{3}$-$\frac{1}{3}$π.
点评 此题是圆的综合题,其中涉及到切线的判定与性质,等边三角形的判定与性质,直角三角形的性质,扇形面积的求法和作复杂图形,根据已知得出正确图形是解题关键.

练习册系列答案
相关题目
12.函数y=x2+3x-4的图象与y轴的交点坐标是( )
| A. | (2,0) | B. | (-2,0) | C. | (0,4) | D. | (0,-4) |
9.已知(x2+y2+1)(x2+y2+3)=8,则x2+y2的值为( )
| A. | -5或1 | B. | 5或-1 | C. | 5 | D. | 1 |
7.下列函数中属于二次函数的是( )
| A. | y=2x-1 | B. | y=ax2-1 | C. | y=2(x-1)2-2x2 | D. | y=(x-1)($\sqrt{2}x+π$) |
 将一长方形纸条按如图所示折叠,∠2=55°,则∠1=70°.
将一长方形纸条按如图所示折叠,∠2=55°,则∠1=70°.