题目内容
10. 如图,以AB为直径的⊙O经过点C,过点C作⊙O的切线交AB的延长线于点P,D是⊙O上于点,且$\widehat{\widehat{BC}}$=$\widehat{CD}$,弦AD的延长线交切线PC于点E,连接AC.
如图,以AB为直径的⊙O经过点C,过点C作⊙O的切线交AB的延长线于点P,D是⊙O上于点,且$\widehat{\widehat{BC}}$=$\widehat{CD}$,弦AD的延长线交切线PC于点E,连接AC.(1)求∠E的度数;
(2)若⊙O的直径为5,sinP=$\frac{3}{5}$,求AE的长.
分析 (1)连接OC.根据等腰三角形的性质得到∠OAC=∠OCA.∠OAC=∠CAD.推出OC∥AE.根据平行线的性质得到∠E=∠OCP.根据切线的性质即可得到结论;
(2)解直角三角形即可得到结论.
解答 解: (1)连接OC.
(1)连接OC.
∵OA=OC,
∴∠OAC=∠OCA.
∵BC=CD,
∴∠OAC=∠CAD.
∴∠OCA=∠CAD,
∴OC∥AE.
∴∠E=∠OCP.
∵PE是的切线,C为切点,
∴∠OCP=90°.
∴∠E=90°;
(2)在Rt△ABD中,OC=2.5,sin∠P=$\frac{OC}{OP}$=$\frac{3}{5}$,
∴OP=$\frac{25}{6}$,
在Rt△APE中,AP=$\frac{25}{6}$+2.5=$\frac{20}{3}$,sin∠P=$\frac{AE}{AP}$=$\frac{3}{5}$,
∴AE=4.
点评 本题考查了切线的性质,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
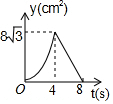
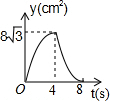
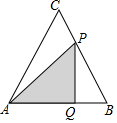 如图,等边△ABC中,AB=8cm,动点P以2cm/s的速度从点A开始,沿边AC、CB的方向匀速运动至点B停止,PQ⊥AB于点Q,则运动过程中△APQ的面积y(cm2)关于点P的运动时间x(s)的函数图象大致是( )
如图,等边△ABC中,AB=8cm,动点P以2cm/s的速度从点A开始,沿边AC、CB的方向匀速运动至点B停止,PQ⊥AB于点Q,则运动过程中△APQ的面积y(cm2)关于点P的运动时间x(s)的函数图象大致是( )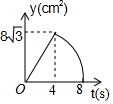
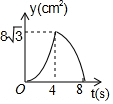

 如图,在平面直角坐标系中,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是x>2.
如图,在平面直角坐标系中,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是x>2.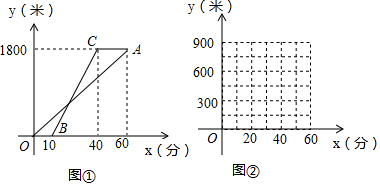
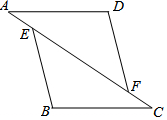 如图,在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.求证:DF=BE.
如图,在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.求证:DF=BE.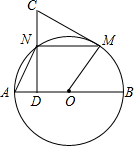 如图,AB为圆O的直径,点M为圆上不与A,B重合的动点,点N平分弧AM,ND⊥AB于点D,过点M的切线交DN的延长线于点C.
如图,AB为圆O的直径,点M为圆上不与A,B重合的动点,点N平分弧AM,ND⊥AB于点D,过点M的切线交DN的延长线于点C.