Question

2．甲、乙两人从学校沿同一路线到距学校1800米的图书馆看书．甲先出发，他们距学校的路程y（米）于甲的行走时间x（分）的函数图象如图①所示．根据图象解答下列问题：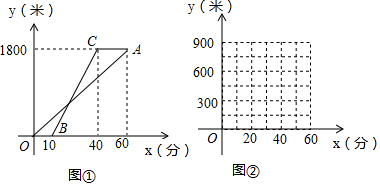

（1）求甲行走的速度．
（2）求直线BC所对应的函数表达式．
（3）设甲、乙两人之间的距离为z（米）．
①当x=10时，z=300；当x=40时，z=600．
②在图②中划出z与x之间的函数图象．

Answer 1

分析 （1）根据图①中的数据可以得到甲行走的速度；
（2）根据图①中的数据可以得到直线BC所对应的函数表达式；
（3）①根据题意和图象中的数据可以分别得到x=10和x=40时对应的z的值；
②根据图象可以求得两人距离为0时的时刻和①中的答案可以画出z于x之间的函数图象．

解答 解：（1）由图象可得，
甲行走的速度为：1800÷60=30米/分，
甲行走的速度为30米/分；

（2）设直线BC所对应的函数表达式为y=kx+b，
$\left\{\begin{array}{l}{10k+b=0}\\{40k+b=1800}\end{array}\right.$，
解得，$\left\{\begin{array}{l}{k=60}\\{b=-600}\end{array}\right.$，
即直线BC所对应的函数表达式为y=60x-600；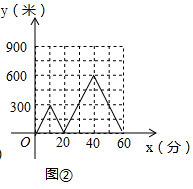

（3）①当x=10时，甲走的路程为：30×10=300，乙行走的路程为0，
∴z=300-0=300，
当x=40时，甲走的路程为：30×40=1200，乙走的路程为1800，
∴z=1800-1200=600，
故答案为：300，600；
②令30x=60x-600，得x=20，
z与x之间的函数图象如右图所示；

点评 本题考查一次函数的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用函数的思想和数形结合的思想解答．