题目内容
4.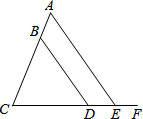 如图,AE∥BD,∠CBD=57°,∠AEF=125°,求∠C的度数.
如图,AE∥BD,∠CBD=57°,∠AEF=125°,求∠C的度数.
分析 先根据平行线的性质求出∠BDE的度数,再由三角形外角的性质即可得出结论.
解答 解:∵AE∥BD,∠AEF=125°,
∴∠BDE=∠AEF=125°.
∵∠BDE是△CBD的外角,∠CBD=57°,
∴∠C=∠BDE-∠CBD=125°-57°=68°.
点评 本题考查的是平行线的性质,熟知两直线平行,同位角相等是解答此题的关键.

练习册系列答案
相关题目
2. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )| A. | 35° | B. | 40° | C. | 50° | D. | 65° |
9.-5的相反数是( )
| A. | 5 | B. | ±5 | C. | -5 | D. | $\sqrt{5}$ |
13.同一平面内,两条不重合的直线的位置关系是( )
| A. | 平行或垂直 | B. | 平行或相交 | C. | 平行、相交或垂直 | D. | 相交 |
14.把方程3x+2y=4,化为用含字母y的代数式表示x的形式正确的是( )
| A. | y=-$\frac{3}{2}$x+2 | B. | y=$\frac{3}{2}$x-2 | C. | x=-$\frac{2y+4}{3}$ | D. | x=$\frac{4-2y}{3}$ |
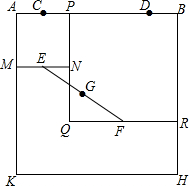 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )