题目内容
3.△ABC三边a,b,c满足a2+b+|$\sqrt{c-2}$-2|=10a+2$\sqrt{b-4}$-22,△ABC为( )| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
分析 由于a2+b+|$\sqrt{c-2}$-2|=10a+2$\sqrt{b-4}$-22,等式可以变形为a2-10a+25+b-4-2$\sqrt{b-4}$+1+|$\sqrt{c-2}$-2|=0,然后根据非负数的和是0,这几个非负数就都是0,就可以求解.
解答 解:∵a2+b+|$\sqrt{c-2}$-2|=10a+2$\sqrt{b-4}$-22,
∴a2-10a+25+b-4-2$\sqrt{b-4}$+1+|$\sqrt{c-2}$-2|=0,
即(a-5)2+($\sqrt{b-4}$-1)2+|$\sqrt{c-2}$-2|=0,
根据几个非负数的和为0,则这几个非负数同时为0,得a=5,b=5,c=6.
故该三角形是等腰三角形.
故选A.
点评 本题主要考查了非负数的性质,难度适中,解题时利用了:几个非负数的和为0,则这几个非负数同时为0.注意此题中的变形要充分运用完全平方公式.

练习册系列答案
相关题目
18. 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )| A. | $\sqrt{12}$ | B. | $\sqrt{10}$ | C. | $\sqrt{8}$ | D. | $\sqrt{6}$ |
15. 如图,在△ABC中,AB=3,AC=$\frac{9}{4}$,点D是BC边上的一点,AD=BD=2DC,设△ABD与△ACD的内切圆半径分别为r1,r2,那么$\frac{r_1}{r_2}$=( )
如图,在△ABC中,AB=3,AC=$\frac{9}{4}$,点D是BC边上的一点,AD=BD=2DC,设△ABD与△ACD的内切圆半径分别为r1,r2,那么$\frac{r_1}{r_2}$=( )
 如图,在△ABC中,AB=3,AC=$\frac{9}{4}$,点D是BC边上的一点,AD=BD=2DC,设△ABD与△ACD的内切圆半径分别为r1,r2,那么$\frac{r_1}{r_2}$=( )
如图,在△ABC中,AB=3,AC=$\frac{9}{4}$,点D是BC边上的一点,AD=BD=2DC,设△ABD与△ACD的内切圆半径分别为r1,r2,那么$\frac{r_1}{r_2}$=( )| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
10.一件工作,甲单独做要20小时完成,乙单独做要12小时完成,现在由甲单独做4小时,剩下的部分由甲、乙合做,那么剩下的部分需要几个小时完成?若设还要xh完成,则依题意可列方程为( )
| A. | $\frac{4}{20}-\frac{x}{20}-\frac{x}{12}=1$ | B. | $\frac{4}{20}-\frac{x}{20}+\frac{x}{12}=1$ | C. | $\frac{4}{20}+\frac{x}{20}-\frac{x}{12}=1$ | D. | $\frac{4}{20}+\frac{x}{20}+\frac{x}{12}=1$ |
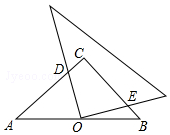 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AC=1,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=1.
如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AC=1,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=1.