题目内容
14.如图1,A(0,-1),A、C关于x轴对称,AB=2,EF∥BC,交AB的延长线于E点,交y轴于F点.(1)求∠AEF;
(2)如图2,将△AEF绕A点顺时针旋转得到△APQ,PQ分别交y轴于M,交BC延长线于D点,PA交BC于H点,当D(m,2)时,问AM+DH大小是否变化并证明.
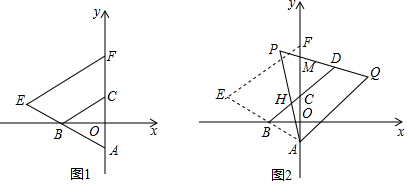
分析 (1)先利用锐角三角函数即可得出∠BAO=60°,进而得出△ABC是等边三角形,最后用平行线的性质即可得出结论;
(2)先用待定系数法求出直线BC解析式,即可得出点D坐标,进而求出CD=2,根据∠DCM=60°构造出等边三角形,进而判断出△ACH≌△DMN,最后代换即可得出结论.
解答 解:(1)∵A(0,-1),
∴OA=2,
在Rt△AOB中,AB=2,OA=1,
∴cos∠BAO=$\frac{OA}{AB}$=$\frac{1}{2}$,
∴∠BAO=60°,
∵A、C关于x轴对称,
∴C(0,1),
∴AC=2=AB,
∴△ABC是等边三角形,
∴∠ABC=60°,
∵EF∥BC,
∴∠AEF=∠ABC=60°;
(2)AM+DH大小不发生变化,
理由:如图,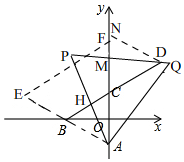 在Rt△AOB中,AB=2,OA=1,根据勾股定理得,OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{3}$,
在Rt△AOB中,AB=2,OA=1,根据勾股定理得,OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{3}$,
∴B(-$\sqrt{3}$,0),
∵C(0,1),
∴直线BC的解析式为y=$\frac{\sqrt{3}}{3}$x+1,
∵D(m,2)在直线BC上,
∴$\frac{\sqrt{3}}{3}$m+1=2,
∴m=$\sqrt{3}$,
∴D($\sqrt{3}$,2),
∴CD=$\sqrt{3+(2-1)^{2}}$=2,
由(1)知,△ABC是等边三角形,
∴∠ACB=∠ABC=60°,
在AC上取一点N使CN=CD=2,
∴△CDN是等边三角形,
∴DN=CD=2,∠DNM=∠CDN=60°=∠ACH,
∴∠PDB+∠PDN=60°,
∵△AEF绕A点顺时针旋转得到△APQ,
∴∠P=∠AEF=60°=∠ABC,
∵∠DHP=∠AHB,
∴∠PAB=∠PDB,
∴∠PDN+∠PAB=60°,
∵∠BAC=60°,
∴∠PAC+∠PAB=60°,
∴∠PAC=∠PDN,
∵AC=2=DN,
在△ACH和△DMN中,$\left\{\begin{array}{l}{∠ACH=∠DNM=60°}\\{AC=DN}\\{∠CAH=∠NDM}\end{array}\right.$,
∴△ACH≌△DMN(ASA),
∴CH=MN.
∴AM=AN-MN=CN+AC-MN=2+2-MN=4-MN,
∵DH=CD+CH=2+MN,
∴AM+DH=4-MN+2-MN=6.
即:AM+DH不发生变化,是定值为6.
点评 此题是几何变换综合题,主要考查了旋转的性质,锐角三角函数,等边三角形的判定和性质,全等三角形的判定和性质,待定系数法,勾股定理等知识点;构造出等边△CDN是解本题的关键.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案| 收费方式 | 月使用费(元) | 包时上网时间(h) | 超时费(元/min) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
(Ⅰ)用含有x的式子填写表格:
| 0≤x<25 | 25<x≤50 | x>50 | |
| 收费方式A应收取费用(元) | 30 | 3x-45 | 3x-45 |
| 收费方式B应收取费用(元) | 50 | 50 | 3x-100 |
 如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )
如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )| A. | a=c | B. | 当a=b=c时,四边形BEDF是菱形 | ||
| C. | $\frac{AF}{AB}$=$\frac{a}{a+b}$ | D. | 正方形ABCD面积为(a+b)2+c2 |
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
| A. | 6x5 | B. | 2x6 | C. | -2x6 | D. | -6x5 |
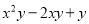 ==______________.
==______________.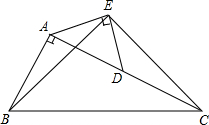 已知:如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,以AD为斜边在△ABC外作等腰直角三角形AED,连结BE、EC.试猜想线段BE和EC有何关系,并证明你的猜想.
已知:如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,以AD为斜边在△ABC外作等腰直角三角形AED,连结BE、EC.试猜想线段BE和EC有何关系,并证明你的猜想.