题目内容
18. 如图,在△ABC中,AB=BC,∠ABC=90°,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是10.
如图,在△ABC中,AB=BC,∠ABC=90°,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是10.
分析 首先作B关于AC的对称点D,连接AD,ED,则ED交于AC于点P,此时PB+PE最小,然后由在△ABC中,AB=BC,∠ABC=90°,可得∠BAD=90°,又由BE=2,AE=3BE,可求得AE与AD的长,继而求得PE+PB=DE的长.
解答 解:作B关于AC的对称点D,连接AD,ED,则ED交于AC于点P,此时PB+PE最小,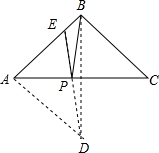 则PB=PD,∠BAC=∠DAC,AD=AB,
则PB=PD,∠BAC=∠DAC,AD=AB,
∵在△ABC中,AB=BC,∠ABC=90°,
∴∠BAC=45°,
∴∠DAC=∠BAC=45°,
∴∠BAD=90°,
∵BE=2,AE=3BE,
∴AE=6,AB=AE+BE=8,
∴DE=$\sqrt{A{E}^{2}+A{D}^{2}}$=10,
∴PB+PE=PD+PE=DE=10.
故答案为:10.
点评 此题考查了最短路径问题以及等腰直角三角形性质.注意找到点P的位置是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,BC⊥AC,AB⊥BD,且BC=4,AC=3,AB=5,BD=12,AD=13,则点D到AB的距离是12,点A到BC的距离是3.
如图,BC⊥AC,AB⊥BD,且BC=4,AC=3,AB=5,BD=12,AD=13,则点D到AB的距离是12,点A到BC的距离是3.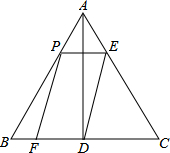 如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连接ED,以PE、ED为邻边作平行四边形PEDF.设线段AP的长为x(0<x<6).
如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连接ED,以PE、ED为邻边作平行四边形PEDF.设线段AP的长为x(0<x<6).
 如图,为了测量一个池塘的宽BC,小明在池塘一侧的平地上选一点A,再分别找出线段AB,AC的中点D,E,若小明测得DE的长是20米,则池塘宽BC=40米.
如图,为了测量一个池塘的宽BC,小明在池塘一侧的平地上选一点A,再分别找出线段AB,AC的中点D,E,若小明测得DE的长是20米,则池塘宽BC=40米. 已知:如图,在△ABC中,D、E分别是AB、BC边上的中点,过点C作CF∥AB,交DE的延长线于F点,连接CD、BF.
已知:如图,在△ABC中,D、E分别是AB、BC边上的中点,过点C作CF∥AB,交DE的延长线于F点,连接CD、BF. 如图,将三角形ABC水平向右平移得到三角形DEF,A,D两点的距离为1,CE=2,∠A=72°,则:
如图,将三角形ABC水平向右平移得到三角形DEF,A,D两点的距离为1,CE=2,∠A=72°,则: