题目内容
如图，Rt△ABC的硬纸片，∠BAC=90°，AB=3，BC=5，AD为BC边上的高，从这张硬纸片剪下一个如图所示的内接正方形EFGH，则正方形EFGH的边长为考点：相似三角形的应用
专题：
分析：根据题意得出三角形的高AD的长，再利用相似三角形的判定与性质得出即可．
解答：解：∵∠BAC=90°，AB=3，BC=5，
∴AC=4，
∴AB×AC=AD×BC，
则AD=
=
，
∵HG∥BC，
∴△AHG∽△ABC，
∴
=
，
设正方形边长为x，则
=
，
解得：x=
．
故答案为：
．
∴AC=4，
∴AB×AC=AD×BC，
则AD=
| AB×AC |
| BC |
| 12 |
| 5 |
∵HG∥BC，
∴△AHG∽△ABC，
∴
| AD-HE |
| AD |
| HG |
| BC |
设正方形边长为x，则
| ||
|
| x |
| 5 |
解得：x=
| 60 |
| 37 |
故答案为：
| 60 |
| 37 |
点评：此题主要考查了相似三角形的判定与性质，得出△AHG∽△ABC是解题关键．
练习册系列答案
相关题目
若式子
的值比
的值大2，则x的值为（ ）
| x-1 |
| 4 |
| 2-x |
| 3 |
| A、1 | B、5 | C、-5 | D、11 |
如图，篱笆（虚线部分）的长度是15cm，如何围篱笆才能使所围矩形的面积最大．
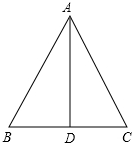如图，在△ABC中，AB=AC，AD是∠BAC的平分线，BD=2cm，求BC的长和∠ADC的大小．
如图，已知AB是直径，弦CD与AB相交于点P，且将AB分成2和8两段，∠DPB=30°，求弦CD的长．